Análise Matemática I - Física, Engª Física, Engª Química, Engª Geológica, Engª Geográfica, Engª Minas
![]()
![]()
3 de Fevereiro de 1998
Duração: 3 horas
Sem consulta de apontamentos ou textos
Tabela autorizada
Calculadora científica ou gráfica autorizada
1- Considere a correspondência g definida por:
g(x) = y tal que ![]()
a) Mostre que define uma função e determine o seu domínio e contradomínio;
b) Prove que g não é a função arcsen;
c) Relacione a função g com a função arcsen.
2- Considere a função real de variável real definida por
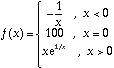
a) Indique, justificando adequadamente:
i) Os pontos de descontinuidade, caso existam;
ii) A função primeira derivada;
iii) A monotonia e os extremos relativos, caso existam;
iv) As equações das assímptotas, caso existam;
v) As concavidades e os pontos de inflexão, caso existam.
b) Esboce o gráfico de ![]() , indicando no gráfico onde estão representadas cada uma das propriedades obtidas na alínea anterior.
, indicando no gráfico onde estão representadas cada uma das propriedades obtidas na alínea anterior.
c) Obtenha a função primitiva de ![]() caso exista e caso seja possível obtê-la como soma finita de funções elementares.
caso exista e caso seja possível obtê-la como soma finita de funções elementares.
3- Calcule
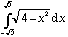
fazendo a substituição ![]() = 2 sen t
= 2 sen t
4- Calcule:
a) 
b) 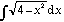
c) 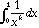 (k é uma constante real positiva)
(k é uma constante real positiva)
5- O número de bactérias numa cultura aumenta de 600 para 1800 em duas horas. Supondo que a taxa de variação do número de bactérias seja directamente proporcional ao número de bactérias presente, determine:
a) Uma fórmula segundo a qual possamos obter o número de bactérias nessa cultura em cada instante ![]() .
.
b) O número de bactérias ao fim de 4 horas.
6- Encontre uma função 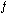 contínua em
contínua em
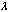 de modo que, para todo o
de modo que, para todo o  real, se tenha:
real, se tenha:
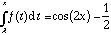
7- a) Mostre que a fórmula da primitivação por partes se pode obter da fórmula da derivação de um produto de duas funções.
b) As imagens seguintes mostram a utilização de uma calculadora gráfica para traçar o gráfico de uma curva definida em coordendas polares por ![]() :
:
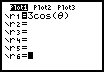
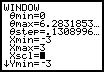
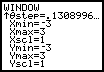
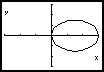
Faça as observações que entender adequadas sobre a eficácia e correcção deste procedimento.