Summer School on Orthogonal Polynomials and Special Functions:

Orthogonal Polynomials

Approximation Theory

Iteration theory

Matrix moment problems

Birth and death processes

Integral Transforms

Number Theory

Cultural Program

This year Coimbra is the portuguese capital of culture.
Every day there will be a visit to the old part of Coimbra University.
The wednesday afternoon are free of lectures, and we plan a visit to the Roman town of Conimbriga (12 Km far from Coimbra) and the old part of our University, and by night we have a conference dinner.

Travel Information

Coimbra can easily be reached by car (close to the highway A1, Lisbon-Porto) and train (200 km from Lisbon International Aiport and 100 km from Porto International Airport).

The railway station you have to take, if you come by plane is Campanhã in Porto and Gare do Oriente in Lisbon. See train schedules at the web page CP-schedules and prices at CP-prices.

The university has experience in organizing conferences. Furthermore the Summer Course is planned during the academic holiday so that there is no interference with regularly scheduled classes or seminars.

Accommodation

The participants stay in Hotels IBIS and Almedina, and Residenciais Alentejana, Antunes and Botânico.

Hotel	Single	Double	Triple	Address	Phone
Residencial Alentejana	33€	43€		R. Dr. Henrique Seco, 1	+351 239825924
Residencial Antunes	34,5€	43,10€	54€	R. Castro Matoso, 8	+351 239854720
Residencial Botânico	34,5€	39€		R. Bairro de S. José, 15	+351 239714824
Hotel IBIS	48,74€			R. Emídio Navarro	+351 239852130
Hotel Almedina	42,35€	50,16€		R. Fernão de Magalhães, 199	+351 239855500

The Organizing Committee

The local organizing committee for this summer school consists of:

Amílcar Branquinho, Departamento de Matemática da Universidade de Coimbra, Coimbra, Portugal.

Ana Foulquié, Departamento de Matemática da Universidade de Aveiro, Aveiro, Portugal.

The scientific committee, acting for the whole series of summer schools 2001-2004 consists of:

Amílcar Branquinho, Universidade de Coimbra, Portugal

Erik Koelink, Technische Universiteit Delft, the Netherlands

Rupert Lasser, GSF-Forschungszentrum für Umwelt und Gesundheit and Technische Universität München, Germany

Francisco Marcellán, Universidad Carlos III de Madrid, Spain

Walter Van Assche, Katholieke Universiteit Leuven, Belgium

Lecturers

C. Berg (Kobenhavns Universitet, Kobenhavn, Denmark): Matrix moment problems.

J. Bustoz* (Arizona State University, USA): Classical summability theory and q-series.

G. López Lagomasino (Universidad Carlos III de Madrid, Madrid, Spain): Constructive theory of approximation.

F. Marcellán (Universidad Carlos III de Madrid, Spain): Orthogonal polynomials and Sobolev inner products.

F. Peherstorfer (Johannes Kepler Universität Linz, Linz, Austria): Iteration theory and orthogonal polynomials.

W. Van Assche (Katholieke Universiteit Leuven, Belgium): Analytic Number Theory.

E. Van Doorn (Universiteit Twente, Enschede, the Netherlands): Birth and death processes and orthogonal polynomials.

S. Yakubovich (Universidade do Porto, Portugal): Integral Transforms of Hypergeometric Functions.

*Due to health problems Professor Joaquin Bustoz cannot present the course "Classical summability theory and q-series". The organizing committee wishes him a quick recover and hopes that in one of the next meetings he will be again among the participants.

Work Program: Room Pedro Nunes in the Department of Mathematics, School of Sciences and Technology, University of Coimbra

First Week

	Monday	Tuesday	Wednesday	Thursday	Friday
Opening session	9h-9h25m
Christian Berg	9h30m-11h30m	9h-11h	9h-11h	9h-11h	9h-11h
coffee break	11h30m-12h 16h-16h20m	11h-11h30m 16h-16h20m	11h-11h30m	11h-11h30m 16h-16h20m	11h-11h30m 16h-16h20m
Erik Van Doorn	12h-13h 15h-16h	11h30m-13h30m	11h30m-13h30m	11h30m-13h30m	11h30m-13h30m
lunch	13h-15h	13h30m-15h	13h30m-14h30m	13h30m-15h	13h30m-15h
Semyon Yakubovich		15h-16h 16h20m-17h20m			15h-16h 16h20m-17h20m
Short Communication	16h20m-18h: 5,6	17h20m-18h: 2		15h-16h: 10,11 16h20m-18h: 4,7	17h20m-18h: 12
cultural program			14h30m-18h

Room José Anastácio da Cunha

Second Week

	Monday	Tuesday	Wednesday	Thursday	Friday
Guillermo López Lagomasino	9h-11h	9h-11h	9h-11h	9h-11h	9h-11h
coffee break	11h-11h30m 16h-16h20m	11h-11h30m 16h-16h20m	11h-11h30m	11h-11h30m 16h-16h20m	11h-11h30m 16h-16h20m
Franz Peherstorfer	11h30m-13h30m	11h30m-13h30m	11h30m-13h30m	11h30m-13h30m	11h30m-13h30m
lunch	13h30m-15h	13h30m-15h	13h30m-14h30m	13h30m-15h	13h30m-15h
Walter Van Assche	15h-16h	15h-16h		15h-16h	15h-16h
Francisco Marcellán	16h20m-17h20m	16h20m-17h20m		16h20m-17h20m	16h20m-17h20m
Short Communication	17h20m-18h: 8	17h20m-18h: 3		17h20m-18h: 9	17h20m-18h: 1
cultural program			14h30m-18h

Abstracts

Author: Christian Berg

Title: Matrix Moment Problems

Abstract:

Complex measures and matrix.valued measures.

Compact sets of positive matrix-valued measures.

Krein's Theorem characterizing matrix moment sequences.

Matrix inner products and orthonormal matrix polynomials.

Indeterminate matrix moment problems and N-Jacobi matrices.

Author: Joaquin Bustoz

Title: Classical summability theory and q-series

Abstract: The classical theory of summability was an important area of research from about 1900 to about 1960. Although there is still very good work being done in the subject, there has been a substantial reduction in interest. In these lectures we will give a brief overview of classical results including Hausdorff summability and Gronwall summability. We will discuss applications to trigonometric Fourier series and to univalent functions. Next we will discuss recent developments in ''q-Fourier series'' on both q-quadratic and q-linear grids. Then we will establish connections between q-series and classical summability methods that produce new methods of summability. We will give some applications of these q-summability methods and finish with some open questions.

Author: Guillermo López Lagomasino

Title: Constructive Theory of Approximation

Abstract:

Padé approximation. Definition and basic properties.

Hadamard´s Theorem on the radii of m-meromorphy of an analytic function.

Montessus de Ballore's Theorem on the location and order of poles.

Inverse problems for row sequences of Padé approximants.

Possible extensions of the previous results to multipoint Padé approximants, orthogonal expansions and expansions in terms of Faber polynomials.

Theorems of Markov and Stieltjes on the convergence of diagonal Padé approximants.

Inverse problems for diagonal sequences of Padé approximants. Gonchar´s Theorem.

Extension of the Theorems of Markov. Stieltjes and Gonchar to other types of expansions.

Author: Francisco Marcellán

Title: Orthogonal polynomials and Sobolev inner products

Abstract: An introduction to the recent trends and main results in the theory of orthogonal polynomials with respect to Sobolev inner products is the aim of this set of lectures. We will focus our attention in some open problems. Lecture notes with self-contained exercises will be provided to the participants in the summer school.

Standard orthogonality versus orthogonality with respect to Sobolev inner products.

Multiplication operator in Sobolev spaces. Some applications to the location of zeros of orthogonal polynomials.

Asymptotic properties of Sobolev orthogonal polynomials.

Differential operators in Sobolev spaces. Regular and singular second order boundary value problems.

Fourier expansions and Sobolev orthogonal polynomials.

Author: Franz Peherstorfer

Title: Lectures on Iteration of functions and orthogonal polynomials

Abstract:

Part I: Iteration of one dimensional maps.

Periodic points and stable sets: Theorem of Li-Yorke ( = "Period 3 implies chaos''), Theorem of Sharkovskii (existence and order of periodic points) and Theorem of Singer (Schwarz's derivative and the maximal number of attracting cycles).
Bifurcation: Important types of bifurcations as pitchfork, saddle node and period doubling bifurcations Example: family of logistic functions.
Chaotic maps:

(a) Definition, sensitive dependence on initial conditions, Lyapunov exponents;

(b) Symbolic dynamics and conjugacy;

(c) Investigation of the chaotic behaviour of the logistic function, consequences for population models. Unimodal functions and the Feigenbaum constant;

(d) Invariant measures-Perron Frobenius Operator, Orthogonal polynomials.

Part II: Julia and Mandelbrot set

Iteration of polynomials and of rational functions in the complex plane:

(a) Julia set - periodic points - family of normal functions;

(b) How to get the Julia set;

(d) Orthogonal and extremal polynomials on sets invariant under a polynomial map, in particular on Julia sets.

Two dimensional maps:

(a) Nonlinear maps and Jacobian matrix

(b) Stable and unstable manifolds

(d) Connection between differential equations and discrete dynamical systems: the Poincaré map.

Author: Walter Van Assche

Title: Analytic Number Theory

Abstract: In this course we will cover some aspects of analytic number theory, in particular rational approximation of irrational numbers, irrationality proofs and transcendence proofs. Quite often the construction of rational approximants to real numbers is by means of continued fractions, Padé approximation or Hermite-Padé approximation. The following topics will be covered:

Continued fractions in number theory.

Algebraic and transcendental numbers.

Irrationality proofs; irrationality of e and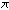

Padé approximation.

Irrationality of

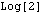and q-extensions of the harmonic series.

Hermite-Padé approximation.

Irrationality of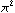

, and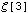

Transcendence proofs; transcendence of e.

Irrationality measures; Roth's theorem.

Author: Erik van Doorn

Title: Orthogonal Polynomials and Birth-Death Process

Abstract: The course will be an introduction to the theory of birth-death processes with emphasis on the role played by orthogonal polynomials in the analysis of these processes. The general theme of the course will be the phenomenon that the problem of extracting certain information about a birth-death process from the parameters defining the process can often be translated into a problem extracting information about a set of orthogonal polynomials and the associated measure from the parameters in the recurrence relation satisfied by these polynomials.

Topics addressed in the course include: birth-death polynomials, the Karlin-McGregor (or spectral) representation, recurrence and transience, ratio limits, exponential ergodicity, speed of convergence to stationarity, quasi-stationarity, limiting conditional distributions, first entrance and return times, random walks (discrete-time birth-death processes), birth-death fluid models.

Many examples will be given to illustrate the concepts and results.Abstract: The course will be an introduction to the theory of birth-death processes with emphasis on the role played by orthogonal polynomials in the analysis of these processes. The general theme of the course will be the phenomenon that the problem of extracting certain information about a birth-death process from the parameters defining the process can often be translated into a problem extracting information about a set of orthogonal polynomials and the associated measure from the parameters in the recurrence relation satisfied by these polynomials.

Many examples will be given to illustrate the concepts and results.

Author: Semyon Yakubovich

Title: Integral Transforms of Hypergeometric Functions

Abstract: The Mellin transform and the notion of hypergeometric functions; Gamma function and the Mellin-Barnes integrals; Bessel functions and classical transforms; Composition method of integral transformations and general 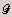-transform; Non-convolution integral transformations; Introduction to the class of the Kontorovich-Lebedev type integral transformations.

References:

Akhiezer, N.I. "Lectures on integral transforms". AMS. 1988. Vol. 70.
Marichev, O. "Handbook of integral transforms of higher transcendental functions, theory and algorithmic tables". Ellis Horwood. 1982.
Yakubovich, S. "Index Transforms", World Scientific, 1996.
Yakubovich, S. and Luchko, Yu. "Hypergeometric approach to integral transforms and convolutions", Kluwer. 1994.

Short Communications

Abrantes,Mário António Grande.

Title. Generating Functions for Several Variables Classical Orthogonal Polynomials.

Abstract.Classical orthogonal polynomials in one variable are the unique set of orthogonal polynomials in one variable which can be defined by a Rodrigues type formula. Using Lagrange formula we can get a generating function for polynomials. In this work, we use an extension of Lagrange formula to polynomial sequences of two variables, to obtain a generating function of the following types of orthogonal polynomial sequences: Hermite×Hermit classical families, circle polynomials and triangular polynomials.

Christiansen, Jacob Stordal.

Title. A moment problem and a family of integral evaluations.

Abstract. The Askey-Wilson integral tells us how to integrate the product of four generating functions for the continuous q-Hermite polynomials times their weight function. In a similar way one can take the product of four generating functions for the q^-1-Hermite polynomials as a starting point. But since the q^-1-Hermite moment problem is indeterminate, infinitely many integrals (with the same value) are coming up, one for each solution to the moment problem. In the talk a new family of weight functions for the q^-1-Hermite polynomials will be presented and the corresponding integrals will be given as well.
A function f(x) with x= sinh y can be viewed as a function of e^y and we shall use the notation $\breve{f}(e^y):=f(x)$. The divided difference operator $\mathcal{D}_q$ defined by \[
\mathcal{D}_qf(x)=\frac{\breve{f}(q^{1/2}e^y)-\breve{f}(q^{-1/2}e^y)}
{(q^{1/2}-q^{-1/2})\cosh y}, \quad x=\sinh y \]
is a lowering operator for the q^-1-Hermite polynomials. In fact, $ \mathcal{D}_q$ is a bounded operator on the weighted L²-spaces in which the q^-1-Hermite polynomials are dense. The right inverse of $\mathcal{D}_q$ can be identified as an integral operator and an explicit expression for the kernel will be derived.

Symmetric coherent pairs were introduced by A. Iserles et al. in 1991, and H. G. Meijer gave a description of them in 1997. Moreover, if (\ref{1}) holds, then we get \begin{equation}\label{2} T_n + s_{n} T_{n-2} = \frac{P'_{n+1}}{n+1} + u_{n} \frac{P'_{n-1}}{n-1}. \end{equation} The aim of our contribution is to describe the moment functional $v$ assuming that $w$ is classical and that the corresponding sequences of monic orthogonal polynomials satisfy (\ref{2}). Then, we obtain a result announced by Sri Ranga and others in 2001.

Costas-Santos, Roberto Santiago.

Title. Number Theory, q-calculus. The Zeta and q-Zeta functions.

Abstract. We give a simple introduction of Number theory and some applications related with cyclothomic polynomials, q-calculus and the Zeta function and its natural q extenssions as well as some identities of these functions. Besides, we give some applications related with this functions.

Delgado Amaro, Antonia María.

Title. On an extension of symmetric coherent pairs of orthogonal polynomials.

Abstract. Given two positive symmetric moment functionals $w,v$ and $\{ P_n \}, \{ T_n \}$ the corresponding sequences of monic orthogonal polynomials for $w,v$ respectively, if they are related by \[ T_n=\frac{P'_{n+1}}{n+1} + u_{n} \frac{P'_{n-1}}{n-1}, \] then the pair $(w,v)$ is said to be a symmetric coherent pair. In this case we can prove that \begin{equation}\label{1} P_n + u_{n} P_{n-2} = Q_n^\lambda + d_{n} Q_{n-2}^\lambda, \end{equation} where $Q_n^\lambda$ are monic orthogonal polynomial with respect to the Sobolev bilinear form $\varphi (p,q)= w(p\,q) + \lambda v(p'\,q')$.

Daruis, Leyla.

Title. Para-Orthogonal Polynomials and Quadrature Formulas on [0,1] .

Abstract. We establish a relation between quadrature formulas on the interval $[ - 1, 1]$, that approximate integrals of the form $J_\mu (F) = \int_{-1}{1} F(x) \mu (x)dx$, and Szegö quadrature formulas on the unit circle that approximate integrals of the form $I (f) =\int_{-1}{1} f (e^{i \theta}) w (\theta) d \theta$. The functions $\mu (x)$ and $w (\theta)$ are assumed to be weight functions on $[ - 1, 1]$ and $[-\pi,\pi]; respectively, and related by $w (\theta) = \mu (cos \theta)|\sin \theta|$. It is well known that the nodes of Szegö formulas are the zeros of the so called para-orthogonal polynomials $B_n (z,\tau) = \Phi_n (z) + \tau \Phi_n^* (z)$, $|\tau|= 1$, $\Phi_n (z)$ and $\Phi_n^*$ being the orthogonal and reciprocal polynomials, respectively, with respect to the weight function $w(\theta)$. Furthermore, for $\tau = \pm 1$ we have recently obtained Gauss-type quadrature formulas on $[ - 1, 1]$. In this work, making use of the para-orthogonal polynomials with $\tau \not= \pm 1$, a one-parameter family of interpolatory quadrature formulas with positive coefficients for $J_\mu (F)$ is obtained. Some illustrative numerical examples are also included.

Eiermann, Michael.

Title. Orthogonal Polynomials in Finite-Dimensional Spaces.

Abstract. Denote by ${\cal P}(a)$ the algebra of all polynomials (with complex coefficients) modulo the monic polynomial $a(\zeta)$ of exact degree $L$. Let further $M$ be a Hermitian positive definite $L$-by-$L$ matrix. We consider the inner product on ${\cal P}(a)$ which is defined by $(\zeta^j,\zeta^k)=M(k,j)$ ($0 \le j,k \le L-1$) and investigate certain properties of the corresponding orthogonal and kernel polynomials. Special emphasis is put on the questions under which conditions these polynomials satisfy short recurrence relations.

Garrido Berenguel, Angeles.

Title. Electrostatic interpretation of zeros of semiclassical orthogonal polynomials.

Abstract. Polynomials orthogonal with respect to a perturbation of certain classical weight functions by the addition of mass points at the end points of the interval $\Omega\subset\mathbb{R}$ are considered. These polynomials satisfy a second order linear differential equation with varying polynomial coefficients depending on $\lambda\in\mathbb{R}^+$. Indeed, such a differential equation leads to an electrostatic problem for $n$ positive charges in the interval with a varying external field and fixed charges at the end points. We show that for $n$ large enough the zeros of the orthogonal polynomials minimize the electrostatic energy for $n$ movable charges in the corresponding electrostatic equilibrium problem.

Inglart, Mélissa.

Title. Asymptotic error estimate for Krylov's subspaces methods.

Abstract. Using the logarithmic potential theory, we study asymptotic error of Krylov subspace methods. We work at the moment on a convection-diffusion equation and especially on the linear system arising from a finite difference discretization, solved with GMRES. First, we study the eigenvalues asymptotic distribution of the preconditioned linear system. Secondly, we use results about constrained energy problems in logarithmic potential theory.

Rebocho, Maria das Neves.

Title. Convergence classes for analytic functions represented by Abel-Goncharov series.

Abstract.The aim of this short communication is to present a study about representation of analytic functions by Abel-Goncharov series. To do this, we begin by introducing Goncharov polynomials and its main properties. Goncharov interpolation problem is refered and we show a theorem by Polya which gives a sufficient condition of convergence to the interpolation problem in the periodic case. Then we show some results about uniqueness and convergence classes of analytic functions which are represented as series whose coefficients are functionals. Some examples are given: Newton series, Abel series and Abel-Goncharov series.

Sánchez-Moreno, Pablo

Title. Entropic Integrals of Special Functions: Airy Function.

Abstract. The asymptotics of special functions other than classical orthogonal polynomials will be discussed in the configuration space, as well as in the "Fourier-transformed" space. Emphasis will be put in the Airy function. This kind of special function naturally describes the quantum-mechanical wave function of the dynamical states of a charged particle moving in a external electric field of homogeneous character.

Sánchez Ruiz, Jorge.

Title. Information Entropy of Gegenbauer Polynomials and Gaussian.

Abstract. During the last decade there has been an intense activity in the study of the information entropies associated to the classical orthogonal polynomials, motivated by their relevance to quantum physics and their close relationship to other interesting mathematical objects, such as the $L^p$-norms or the logarithmic potentials of the polynomials. In a recent paper (V. S. Buyarov et al. 2000) an efficient method was provided for evaluating in closed form the logarithmic potential and the entropy of Gegenbauer polynomials with integer parameter. The application of this method to the polynomial $C_n^{(l)} (x)$ ($l \in \mathbb{N}$) requires the computation by means of recurrence relations of two auxiliary polynomials, $P(x)$ and $H(x)$, of degrees $2l-2$ and $2l-4$, respectively. Here it is shown that $P(x)$ is related to the Christoffel coefficients of the Gaussian quadrature formula for the Gegenbauer weight $w_l(x) = (1-x^2)^{l-1/2}$, and this fact is used to obtain the explicit expression of $P(x)$. From this result, an explicit formula is also given for the polynomial $S(x) = \lim_{n \rightarrow \infty} P \big( 1-x/(2n^2) \big)$, which plays a key role in the study of the asymptotic ($n \to \infty$ with $l$ fixed) behaviour of the entropy.

Stabolas, Ioannis.

Title. Monotonicity properties and inequalities of the zeros of q-associated polynomials.

Abstract. Using a functional analytic method, based on the three terms recurrence relations that the q-associated polynomials satisfy , we present some monotonicity results and inequalities of the zeros of the orthogonal polynomials under consideration. The obtained results unify, generalize and improve previously known results.

Registration

All registrations for the Summer School on Orthogonal Polynomials and Special Functions must be submitted via Web using the electronic registration form, or by fax, mail or email to the Congress Secretariat

Secretária do Euro Summer Course on OPSF 2003, Departamento de Matemática FCT, Universidade de Coimbra, Apartado 3008, 3000 Coimbra, Portugal.
Fax Number: +351 239832568.

using pdf registration form.

List of Participants

Abrantes,Mário António Grande. address. Instituto Politécnico de Bragança, Escola Superior de Tecnologia e de Gestão de Bragança, Ap. 134, 5301-857 Bragança, Portugal.

Alvarez Rocha, Ignacio. address. Universidad Politécnica de Madrid, Dpto. Matematica Aplicada. E.U.I.T. Telecomunicacion. Ctra. de Valencia Km 7. 28031 Madrid, Spain.

Azevedo, José. address. ISCAP-IPP, Travessa das Ribeirinhas, 95, 4430-511 Vila Nova de Gaia, Portugal.

Beckermann, Bernahardt. address. Universite des Sciences et Technologies de Lille 1, UFR de Mathematiques, Bat. M3, USTL, 59655 Villeneuve d'Ascq cedex, France.

Berg, Christean. Address. Kobenhavns Universitet, Kobenhavn, Denmark.

Bouras, Belgacem. address. Faculté de Science de Sfax, I.S.S.A.T Gabes route de Mednine, Tunisia.

Cantero Medina, María José. address. Universidad de Zaragoza, Departamneto de Análisis Económico, Facultad de CCEE y EE. Gran Vía, 2. 50005 Zaragoza, Spain.

Christiansen, Jacob Stordal. address. University of Copenhagen, Universitetsparken 5, 2100 Copenhagen, Denmark.

Costas-Santos, Roberto Santiago. address. Universidad Carlos III, Ave. Universidad, 30, 28911 Leganés-Madrid, Spain.

Cotrim, Luís. address. Escola Superior de Tecnologia e Gestão do I.P.L., Quinta do Seixo lote 1 - 4 Dto 2410 Leiria, Portugal.

Coussement, Jonathan. address. Katholieke Universiteit Leuven, Celestijnenlaan 200 B 3001 Leuven, Belgium.

Daruis, Leyla. address. Universidad de la Laguna, Departamento de Análisis Matemático, Av. Francisco Sánchez, S/N, 38271 La Laguna. Tenerife, Islas Canarias, Spain.

Daems, Evi. address. Katholieke Universiteit Leuven, Celestijnenlaan 200 B 3001 Leuven, Belgium.

Delgado Amaro, Antonia María. address. Universidad Carlos III, Ave. Universidad, 30, 28911 Leganés-Madrid, Spain.

Eiermann, Michael. address. TU Bergakademie Freiberg, Agricolastr. 1, D-09596 Freiberg, Germany.

Freitas, José Orlando G. address. Universidade da Madeira, Departamento de Matemática e Engenharias, Campus Universitário da Penteada 9000-390 Funchal, Portugal.

Garrido Berenguel, Ángeles. address. Universidad Carlos III, Ave. Universidad, 30, 28911 Leganés-Madrid, Spain.

Ghrissi, Abdallah. address. Faculté de Science de Sfax, I.S.S.A.T Gabes route de Mednine, Tunisia.

Helsen, Steff. address. Katholieke Universiteit Leuven, Celestijnenlaan 200 B 3001 Leuven, Belgium.

Hernandez Benitez, Javier. address. Universidad Carlos III, Ave. Universidad, 30, 28911 Leganés-Madrid, Spain.

Inglart, Mélissa. address. Universite des Sciences et Technologies de Lille 1, UFR de Mathematiques, Bat. M3, USTL, 59655 Villeneuve d'Ascq cedex, France.

Krystek, Anna. address. Institute of Mathematics, Wroclaw University, pl. Grunwaldzki 2/4, Poland.

López Lagomasino, Guillermo. address. Universidad Carlos III de Madrid, Madrid, Spain.

López Garcia, Abey. address. Universidad Complutense de Madrid, C/Horizon, 3-I, 6-A, Spain.

Loureiro, Ana. address. Instituto Superior de Engenharia de Coimbra, Rua Pedro Nunes, 3030-199 Coimbra, Portugal.

Marcellán, Francisco. address. Universidad Carlos III de Madrid, Madrid, Spain.

Marques, Jorge. address. Universidade de Coimbra, Faculdade de Economia, Av. Dias da Silva, 165, 3030 Coimbra, Portugal.

Matos, Ana Cristina. address. Universite des Sciences et Technologies de Lille 1, UFR de Mathematiques, Bat. M3, USTL, 59655 Villeneuve d'Ascq cedex, France.

Mendes, Ana Isabel. address. Escola Superior de Tecnologia e Gestão do I.P.L., Quinta do Seixo lote 1 - 4 Dto 2410 Leiria, Portugal.

Mlotkowski, Wojtek. address. Institute of Mathematics, Wroclaw University, pl. Grunwaldzki 2/4, Poland.

Nascimento, Alexandra. address. Escola Superior de Tecnologia e Gestão do I.P.L., Quinta do Seixo lote 1 - 4 Dto 2410 Leiria, Portugal.

Nascimento Sequeira, Alcino. address. Instituto Superior de Engenharia de Coimbra Rua Pedro Nunes - Quinta da Nora 3030-199 Coimbra, Portugal.

Peherstorfer, Franz. address. Johannes Kepler Universitat Linz, Linz, Austria.

Pereira de Sousa, Victor Luís. address. Instituto Politécnico de Bragança, Escola Superior de Tecnologia e de Gestão de Bragança, Ap. 134, 5301-857 Bragança, Portugal.

Pérez Sinusía, Ester. address. Universidad Pública de Pamplona, Campus de Arrosadía s/n Pamplona 31006, Spain.

Petronilho, José carlos. address. Universidade de Coimbra, Departamento de Matemática, FCTUC, Apartado 3008, Portugal.

Postelmans, Kelly. address. Katholieke Universiteit Leuven, Celestijnenlaan 200 B 3001 Leuven, Belgium.

Rebocho, Maria das Neves. address. Universidade da Beira Interior, Departamento de Matemática, Av. Marquês D'Ávila e Bolama, 1, Covilhã.

Salto, Laura. address. Universidad Carlos III, Ave. Universidad, 30, 28911 Leganés-Madrid, Spain.

Sanchez-Lara, Joaquin. address. Universidad de Almeria, Crta. de Sacramento s/n. La Cañada 04120. ALMERIA, Spain.

Sánchez-Moreno, Pablo. address. Universidad de Granada. Instituto "Carlos I" de Física Teórica y Computacional, Facultad de Ciencias. Campus de Fuentenueva, Spain.

Sánchez-Ruiz, Jorge. address. Universidad Carlos III, Ave. Universidad, 30, 28911 Leganés-Madrid, Spain.

Santos, Ana Margarida. address. Universidade de Aveiro, Departamento de Matemática, Campus de Santiago, 3810 Aveiro, Portugal.

Santos Cardoso, José Luis. address. UTAD, Dep. de Matemática, Quinta de Prados, Apartado 1013, 5000-911 VILA REAL.

Srayeb, Nadia. address. Faculté de Science de Sfax, I.S.S.A.T Gabes route de Mednine, Tunisia.

Stabolas, Ioannis. address. University of Patras, Department of Mathematics, University of Patras, Patras 26500, Greece.

Van Assche, Walter. address. Katholieke Universiteit Leuven, Celestijnenlaan 200 B 3001 Leuven, Belgium.

Van Doorn, Erik. address. Faculty of Mathematical Sciences, University of Twente, PO Box 217, 1500 AE Enschede, The Netherlands.

Vanlessen, Maarten. address. Katholieke Universiteit Leuven, Celestijnenlaan 200 B 3001 Leuven, Belgium.

Wielonsky, Franck. address. Universite des Sciences et Technologies de Lille 1, UFR de Mathematiques, Bat. M3, USTL, 59655 Villeneuve d'Ascq cedex, France.

Wozny, Pawel. address. Institute of Computer Science University of Wroclaw, ul. Przemyckiego 20, 51-151 Wroclaw, Poland.

Yakubovich, Semyon. address. Departamento de Matemática Pura da Universidade do Porto, Porto, Portugal.

Zygmunt, Marcin Jakub. address. Institute of Mathematics, Wroclaw University, pl. Grunwaldzki 2/4, Poland.

Contacts

For further questions please contact Amílcar Branquinho or Ana Foulquié.

Sponsors