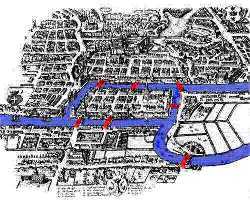
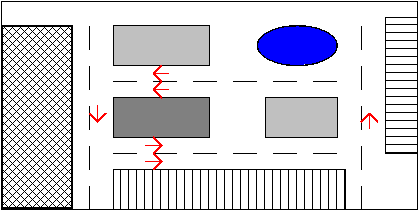
O objectivo principal da ciência aplicada é a de encontrar a melhor maneira para resolver um problema - aquilo a que os matemáticos chamam encontrar a solução óptima. Nalguns casos, poderá ser a maneira mais rápida para concluir um trabalho. Noutras situações, o objectivo poderá ser o maximização do lucro e a minimização dos custos. O que definimos como "óptimo" depende da natureza do objectivo.

Concentremo-nos no problema do controlo de estacionamento numa cidade. Muitas cidades possuem já parquímetros que necessitam ser controlados regularmente pela polícia para evitar as fugas de pagamento. Vamos usar uma cidade imaginária para mostrar como a teoria dos grafos pode ajudar o tornar o controlo de estacionamento mais eficiente.

Consideremos o mapa dado na Figura 1, com estradas, blocos residenciais, espaços verdes, lagos, etc.

Figura 1. Um mapa de estradas numa cidade imaginária.

Existe um sem número de possibilidades para o nosso polícia controlar todos os parquímetros. O nosso trabalho será o de ajudar o chefe da polícia a encontrar a solução óptima, o caminho mais eficiente que deve tomar o seu subalterno, que viaja a pé, por forma a controlar a totalidade dos parquímetros da sua zona.

O chefe da polícia tem dois objectivos em mente: (i) o polícia encarregado de efectuar a vistoria deve percorrer todos os passeios que possuem parquímetros passando duas vezes pelo mesmo passeio o menor número de vezes possível; (ii) o caminho deve começar e acabar no mesmo ponto, por exemplo no sítio onde deixou estacionado o carro.

Poderemos pensar neste problema em termos de uma estrutura chamada grafo, um dos muitos modelos matemáticos que ajuda a simplificar problemas matemáticos complexos.

Na definição anterior usou-se a noção de multiconjunto (a generalização da noção de conjunto que permite a repetição de elementos) por forma a considerar grafos com arestas repetidas, i.e., com mais do que uma aresta entre os mesmos vértices. Na literatura, um grafo com arestas repetidas ou com lacetes (i.e., arestas com extremos incidentes no mesmo vértice) é usualmente chamado um multigrafo. No nosso caso não iremos permitir a existência de lacetes.

Um grafo pode ser usado para representar o nosso mapa de estradas, uma rede de informática, as linhas aéreas, etc.

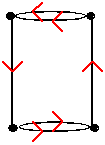
Figura 2. Linhas aéreas

No caso do nosso problema, poderemos representar todo o território a ser patrulhado por um grafo: poderemos pensar cada cruzamento como um vértice e cada passeio com parquímetro como uma aresta.

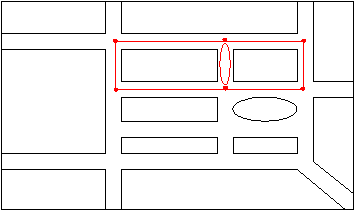
Figura 3a. Um grafo para representar as estradas a percorrer pelo polícia.

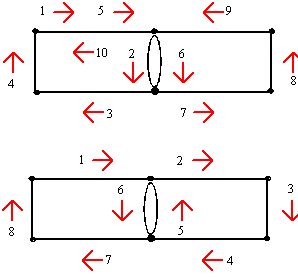
Figura 3b. O mesmo grafo.

Note-se que na Figura 3b, efectuámos uma simplificação ao nosso problema: desprezámos o comprimento das ruas e esquinas.

Figura 4. Dois percursos possíveis.

A Figura 4 mostra-nos dois percursos que o polícia pode tomar para efectuar o controlo. Em ambos os casos o ponto de partida coincide com o ponto de chegada. No entanto, a segunda possibilidade é melhor que a primeira uma vez que neste caso o polícia percorre cada passeio apenas uma única vez.

Antes de prosseguimos a análise do nosso problema, considremos alguns conceitos importantes na teoria dos grafos. Estes conceitos, apesar de apresentados com todo o rigor formal, são bastante simples.

Notemos que, a dimensão |A| de G=(V,A) varia entre 0 e o número de combinações de |V| dois a dois. O valor mais alto para a dimensão é obtido para os chamados grafos completos, isto é, os grafos onde todos os vértices estão ligados entre si.

A dimensão de um caminho/trajecto é também designada por comprimento.

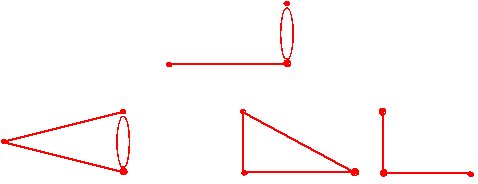
De acordo com a definição anterior, a segunda possibilidade da Figura 4 mostra-nos um circuito de Euler, enquanto que a primeira já não.

Uma das primeiras descobertas da teoria dos grafos foi a de que existem grafos que não possuem quaisquer circuitos de Euler. Por exemplo, alguns dos grafos da Figura 5 não possuem circuitos de Euler.

Figura 5. Quais os grafos que não possuem circuitos de Euler?

Agora que conhecemos as condições que um circuito de Euler deve satisfazer, surgem-nos duas questões óbvias:

1. Existe algum processo efectivo, sem ser por tentativa-erro, para dizer se um grafo particular possui um circuito de Euler?
2. Existe algum método, sem ser por tentativa-erro, para encontrar um circuito de Euler caso ele exista?

Euler respondeu a estas questões em 1735 usando duas noções fundamentais na teoria dos grafos: valência de vértices e grafos conexos.

Como curiosidade, notemos que, a definição anterior é útil para demonstrar o suginte lema (bastante conhecido).

Podemos agora estabelecer o teorema de Euler, a sua resposta simples ao problema de saber quando é que um determinado grafo G possui um circuito de Euler.

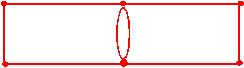
Uma vez determinada a existência de um circuito de Euler num determinado grafo, como encontra-lo? O conjunto de regras que Euler nos deu possuem um interesse teórico e poderão ter um interesse prático se for nosso objectivo programar um computador que encontre mecanicamente os circuitos de Euler num grafo. No entanto, não iremos estudar essas regras uma vez que a maioria dos seres humanos, com um pouco de prática, poderão encontrar circuitos de Euler num grafo por tentativa-erro, mesmo em grafos relativamente grandes.

Munidos agora com o teorema de Euler, vamos olhar de novo para o nosso problema de controlo dos parquímetros. A questão chave é: existe um circuito de Euler no grafo? Poderemos responder a esta questão analisando a conexão do grafo e a valência dos seus vértices. Facilmente se constata o grafo possui um circuito de Euler. O segundo percurso da Figura 4 é um exemplo possível.

E quanto ao problema das pontes de Königsberg que falámos na motivação a este trabalho? Como é fácil de ver, o grafo correspondente a esse problema (ver mapa da cidade de Königsberg) possui todos os seus vértices com valência ímpar. Assim sendo, os habitantes da cidade tinham razão ao concluir que tal percurso era impossível de realizar.

Note-se que foi este problema das pontes que motivou o trabalho de Euler e foi este matemático, ao estabelecer o teorema anterior, que o resolveu de forma eficiente.

O teorema de Euler permite ainda concluir que para cada número natural n, o grafo completo de n vértices tem n(n-1)/2 arestas e, como tal, cada um dos n vértices tem valência n-1. Assim, os circuitos de Euler são possíveis para n=3,5,7,… Este resultado foi estabelecido por Luis Poinsot em 1809.

Posteriormente, em 1849, apareceu um comentário ao trabalho de Poinsot nas "Nouvelles Annales de Mathématiques". Aqui interpretou-se a chamada regra de Poinsot para circuitos de Euler em grafos completos de 7 vértices em termos do jogo de dominó. Se tirarmos os "doubles" (isto é, as peças 0-0, 1-1,…,6-6), as restantes 21 peças correspondem às arestas do grafo completo de 7 vértices e um circuito de Euler representa a sequência das 21 peças com todos os extremos a tocar extremos iguais. Visto que os "doubles" se podem colocar em lugares apropriados, assim que a sequência básica for dada, provámos que o jogo de dominó completo é possível. O número de vezes em que esta situação ocorre é chamado o problema do dominó e foi resolvido em 1871.

Finalmente, como corolário do teorema de Euler, temos ainda o seguinte resultado.

Este resultado nos permite resolver o seguinte problema de carácter lúdico.

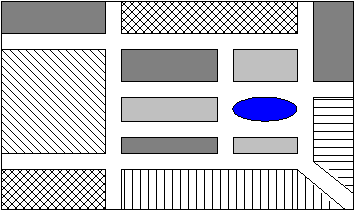
Vejamos agora o que é que o teorema de Euler nos diz em relação ao bairro de três blocos da Figura 6. Na Figura 7 poderemos ver o grafo correspondente (note-se que o passeio sem parquímetros não figura no grafo). Este grafo tem dois vértices com valência ímpar e, como tal, não existem circuitos de Euler para este grafo.

Figura 6. Bairro com três blocos.

Figura 7. Multigrafo correspondente à Figura 6.

Visto que temos que usar duas arestas do grafo mais do que uma vez se quisermos cobrir todas as arestas no nosso circuito, para uma maior eficiência deveremos tornar mínimo o número de repetições que iremos efectuar. Este tipo de problema é chamado muitas vezes o problema do carteiro chinês. No entanto, a teoria dos circuitos de Euler não lida directamente com arestas usadas mais do que uma vez ou arestas de diferentes comprimentos. Teremos de generalizar a teoria para nos ajudar na resolução do problema do carteiro chinês.

Num problema do carteiro chinês real, teremos que ter em conta o comprimento dos passeios, ruas, ou o que quer que as arestas do grafo representem visto que queremos minimizar o total do comprimento das arestas usadas mais do que uma vez. No entanto, vamos começar por simplificar as coisas supondo que as arestas são todas do mesmo comprimento. (Este problema é muitas vezes chamado o problema do carteiro chinês simplificado.) Neste caso temos apenas que contas as arestas que foram usadas mais do que uma vez e não determinar o seu comprimento. Assim, queremos encontrar o circuito que cobre cada aresta e tem o número mínimo de repetições de arestas já cobertas.

A nossa teoria baseia-se na seguinte ideia. Considere um grafo que não possui circuitos de Euler. Nesse caso proceda como se segue:

1. Adicione arestas, duplicando as já existentes, até obter um grafo que seja conexo e possua todos os seus vértices com valência par. Chamamos a este processo a eulerização do grafo uma vez que o grafo obtido possui um circuito de Euler.

2. Encontre um circuito de Euler no grafo eulerizado.

3. Trace esse circuito de Euler no grafo original (antes da eulerização), repetindo o uso de uma aresta sempre que o circuito no grafo eulerizado usa uma aresta adicional.

Agora que aprendemos a eulerizar, o próximo passo é tentar encontrar a melhor eulerização possível. Note-se que existem várias maneiras de eulerizar um grafo. É evidente que, de acordo com a simplificação feita ao nosso problema, encontramos a melhor eulerização se procurarmos a eulerização com o menor número de arestas adicionais. Este requisito extra torna o problema mais interessante mas também mais complicado. Para grafos de grandes dimensões, a melhor eulerização pode não ser óbvia. Poderemos experimentar algumas soluções e escolher a melhor de entre elas. No entanto, poderá haver uma outra solução melhor.

Existe um procedimento sistemático para encontrar a melhor eulerização num grafo mas é complicado. No entanto, com um pouco de prática, a maioria das pessoas pode encontrar a melhor, ou quase a melhor, eulerização usando o processo de tentativa-erro. Este procedimento é especialmente fácil para redes viárias rectangulares.

1.5 Circuitos mais complicados

A teoria que acabámos de expor tem muitas mais aplicações práticas do que o simples controlo dos parquímetros. Sempre que um serviço necessite de ser efectuado ao longo de ruas e estradas, a nossa teoria pode ajudar a fazer o trabalho de forma mais eficiente. Encontramos vários exemplos da aplicabilidade da teoria na colecta do lixo, verificação de contadores eléctricos, etc.

No entanto, cada um destes problemas possui os seus requisitos especiais que apelam a constantes modificações na teoria. Por exemplo, no problema da colecta do lixo, as arestas do nosso grafo representam estradas e não passeios. Se algumas estradas forem de sentido único, teremos que por setas nas respectivas arestas, obtendo assim um grafo orientado (ou grafo direccionado). Os circuitos que procuramos têm que obedecer à orientação do grafo.

Figura 8. Problema da colecta do lixo.

Figura 9. Grafo orientado.

No caso dos varredores de rua, o problema também pode ser modelizado por um grafo orientado. No entanto, existe uma complicação adicional: os carros estacionados. É difícil varrer as ruas com os carros estacionados. Assim, para uma melhor eficiência, são por vezes colocados sinais a especificar quando é que é proibido o estacionamento (por exemplo, às segundas quintas-feiras de cada mês entre as 20 horas e as 2 horas). Assim, neste problema, é importante não só encontrar o circuito de Euler, ou o circuito com o mínimo de duplicações, mas também o circuito que pode ser completo no tempo disponível. Mais uma vez, a teoria pode ser modificada para abarcar este problema.

Finalmente, uma vez que as cidades têm mais do que um varredor, ou camião do lixo, ou controlador de parquímetros, um único circuito não é suficiente. Assim, tem que se dividir o território em várias áreas cada uma a ser percorrida por um circuito. O objectivo genérico será encontrar as soluções óptimas tendo em conta a direcção do tráfego, o número de ruas, as restrições de tempo, etc.

Por exemplo, um estudo piloto efectuado em Nova York em 1970 a propósito dos varredores de rua, permitia poupar cerca de 1.5 milhões de dólares por ano! (Cerca de 225 mil contos.) No entanto a cidade nunca chegou a adoptar esse plano. Uma vez que os serviços prestados têm também que ser encarados de um ponto de vista político, muitos outros factores terão que se ter em linha de conta. Os sindicatos querem defender os empregos dos trabalhadores do município, os burocratas querem manter os orçamentos municipais altos, os políticos não querem ser acusados de medidas impopulares, etc. A cidade perdeu assim uma possibilidade de economizar 1.5 milhões de dólares.

Apesar da complicação dos problemas da vida real, a teoria dos grafos proporciona meios para melhor os entendermos. Os resultados obtidos poderão ter um efeito positivo não só a nível económico como também a nível do bem estar e organização da comunidade.

Para concluir esta secção, apenas um problema final.

Em 1859 o famoso matemático irlandês sir William Rowan Hamilton pôs no mercado um puzzle peculiar. Era construído por um dodecaedro regular. Cada um dos vértices do dodecaedro de Hamilton estava marcado com o nome de uma cidade importante: Bruxelas, Cantão, Deli, Frankfurt, etc. O puzzle consistia em encontrar um caminho ao longo das arestas do dodecaedro por forma a passar por cada cidade apenas uma vez; algumas das primeiras cidades a serem visitadas eram estipuladas de avanço para tornar o problema mais aliciante. Como o dodecaedro era difícil de manobrar, Hamilton produziu uma versão deste jogo em que o dodecaedro era substituído por um grafo planar isomorfo. Não consta que o Dodecaedro de Viagem tivesse tido muito sucesso comercial.

Na secção anterior, vimos que é relativamente simples de determinar se existe um circuito que percorra as arestas de um grafo uma única vez. No entanto, a situação muda radicalmente se fizermos uma mudança aparentemente inócua ao problema: quando é que é possível encontrar um circuito num grafo ao longo das suas arestas que comece e acabe no mesmo vértice e visite cada vértice uma única vez?

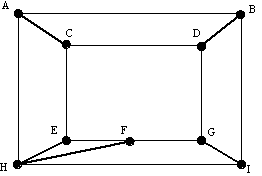
Figura 10. Grafo com vértices rotulados.

Por exemplo, na Figura 10, para obter um circuito que visite os vértices uma única vez poderemos considerar o circuito ABDGIHFECA.

Um percurso tal como o definido anteriormente é chamado ciclo de Hamilton, uma vez que foi Hamilton, quem primeiramente estudou o conceito. (Sabemos agora que o conceito foi descoberto algum tempo antes por Thomas Kirkman, um ministro britânico com queda para a matemática.)

Os conceitos de circuitos de Euler e ciclos de Hamilton são similares naquilo que proíbem voltar a utilizar: nos circuitos de Euler as arestas, nos ciclos de Hamilton os vértices. No entanto, é muito mais difícil determinar quais são os grafos conexos que admitem um ciclo de Hamilton do que determinar os grafos conexos que admitem um circuito de Euler.

Eis algumas regras básicas para encontrar ciclos de Hamilton:

1. Se um vértice tem valência 2, então ambas as arestas incidentes no vértice devem fazer parte do ciclo;

2. Não se deve percorrer um ciclo que não contém todos os vértices;

3. Uma vez que se visite um dado vértice, todas as arestas incidentes nesse vértice que não foram utilizadas podem ser eliminadas.

Os grafos completos, isto é, os grafos onde todos os vértices estão ligados entre si, são hamiltonianos. Assim sendo, dado um grafo G não hamiltoniano, adicionando arestas a G necessariamente se obterá um grafo hamiltoniano.

Notemos que o teorema de Ore não é, como o teorema de Euler, uma condição necessária e suficiente. De facto, o teorema estabelece apenas uma condição suficiente para que um grafo seja hamiltoniano. Notemos ainda que, qualquer grafo nas hipóteses do teorema de Ore é um grafo conexo.

O teorema seguinte resulta imediatamente do anterior. Deixamos a demonstração ao cuidado do leitor.

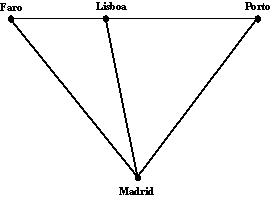
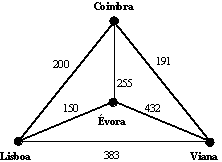
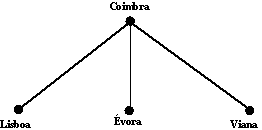
Vimos que, olhando para as valências dos vértices, é possível dizer se um grafo conexo admite ou não um circuito de Euler, mas não temos um método tão simples para nos dizer quando é que um grafo possui um ciclo de Hamilton.

Apesar de apresentarmos o problema do ciclo de Hamilton como uma variante do problema do circuito de Euler, ele possui muitas aplicações em problemas da vida real.

Suponhamos que as inspecções ou as entregas têm de ser feitas em cada vértice (em vez de ao longo de uma aresta) de um grafo. Um caminho "eficiente" no grafo consiste no caminho que passa por todos os vértices uma única vez; isto é, o caminho deverá ser um ciclo de Hamilton. Tais caminhos são úteis para inspeccionar semáforos, ou para entregar o correio, especialmente encomendas postais de grandes dimensões, etc. Existem muitos exemplos similares, mas antes prosseguirmos com os problemas envolvendo aplicações dos ciclos de Hamilton, vamos estudar uma mais importante classe de problemas relacionados.

Suponhamos que é um professor que trabalha em Coimbra. Durante as férias da Páscoa você e um grupo de amigos decidem efectuar uma viagem de carro para visitar outros amigos em Lisboa, Évora e Viana do Castelo. Existem muitas escolhas possíveis no sentido de visitar as cidades de regressar a Coimbra, mas você quer escolher o caminho que minimize a distância que necessita de percorrer. (O problema possuía complicações adicionais se a viagem fosse feita em meios de transporte diferentes.)

Poderemos construir um modelo para a nossa viagem, representando cada cidade a visitar por um vértice de um grafo e o caminho entre cada uma delas por uma aresta. Para completar o modelo, adicionamos um número chamado o peso a cada aresta. O peso representa a distância (em quilómetros) que as separa as cidades representadas pelos vértices que se encontram na extremidade da aresta em causa, ver Figura 11.

Figura 11. Plano de viagem.

Queremos encontrar o caminho de custo mínimo que começa e acaba em Coimbra e visita cada uma das outras cidades uma única vez. Usando a nossa terminologia anterior, queremos encontrar um ciclo de Hamilton de custo mínimo.

Como poderemos determinar qual dos ciclos de Hamilton tem custo mínimo? Existe um algoritmo simples de conceber para este problema:

1. Construa os ciclos de Hamilton que começam em Coimbra.
2. Adicione as distâncias percorridas em cada aresta do ciclo.
3. Escolha o ciclo de distância mínima.

Os passos 2 e 3 do algoritmo são imediatos. Assim, temos que nos preocupar apenas com o primeiro, gerar circuitos Hamiltonianos de forma sistemática. Para encontrar ciclos de Hamilton vamos usar o método das árvores.

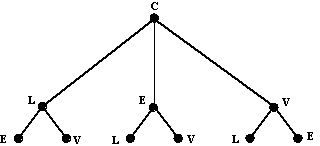
Partindo de Coimbra, poderemos escolher cada uma das três outras cidades para visitar em primeiro lugar. Esta primeira etapa da pesquisa de ciclos de Hamilton é ilustrada na Figura 12.

Figura 12

Se Lisboa for escolhida em primeiro lugar, então existem duas cidades que poderão ser visitadas depois, nomeadamente, Évora e Viana do Castelo. Nesta segunda etapa, no entanto, para cada escolha da cidade a visitar em primeiro lugar, existem duas escolhas desta cidade para a segunda cidade a visitar. Chegamos assim à árvore da Figura 13.

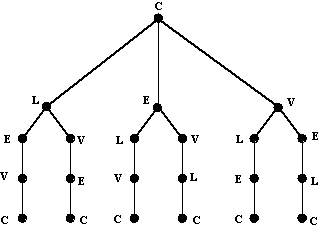
Figura 13

Escolhendo a ordem das primeiras duas cidades a visitar, e sabendo que ciclo de Hamilton as visitas não poder ser repetidas, ficamos apenas com uma escolha para a cidade que falta visitar. Desta cidade regressamos a Coimbra. A árvore completa de todos os percursos possíveis é dada na Figura 14.

Figura 14

Note-se que, uma vez que poderemos percorrer um caminho circular em duas direcções distintas, os percursos enumerados no diagrama da Figura 14 não correspondem a ciclos de Hamilton. Por exemplo, o percurso C-L-E-V-C e o percurso C-V-E-L-C representam o ciclo de Hamilton. Para este problema, no entanto, encontrámos três ciclos de Hamilton distintos entre seis percursos no diagrama da Figura 14.

Note-se ainda que, na construção dos ciclos de Hamilton, não considerámos as distâncias envolvidas. Estivemos apenas interessados nas diferentes hipóteses de fazer a visita. Mas qual é o percurso óptimo? Adicionando as distâncias entre as cidades chegamos facilmente à conclusão que o percurso óptimo é Coimbra, Lisboa, Évora, Viana do Castelo, Coimbra. Neste percurso percorremos 973 quilómetros.

O método das árvores nem sempre é tão fácil de usar como o nosso exemplo sugere. Em vez de fazermos a nossa análise para quatro cidades, consideremos o caso geral de n cidades. O grafo que modela o problema é similar ao da Figura 11 e consiste num grafo pesado com n vértices, com cada par de juntos por uma aresta.

Quantos ciclos de Hamilton existem num grafo completo de n vértices? Poderemos resolver este problema usando o mesmo tipo de análise que efectuamos na contagem dos ramos da árvore. O método usa o chamado princípio fundamental da contagem ou princípio da multiplicação, que diz que existem a possibilidades de escolher uma opção, b possibilidades de escolher uma segunda opção a seguir à primeira, ... ,e z possibilidades de escolher o último item depois das escolhas precedentes, o número total de escolhas possível é: a x b x ... x z.

Assim, a cidade a ser visitada depois da cidade de partida pode ser escolhida de n-1 maneiras, a cidade seguinte de n-2 maneiras, e assim sucessivamente até ficarmos apenas com uma escolha possível. Usando o princípio fundamental da contagem, existem (n-1)!=(n-1)(n-2)...2.1 percursos.

Pares de percursos correspondem ao mesmo ciclo de Hamilton uma vez que cada percurso pode ser percorrido em dois sentidos diferentes. Assim existem (n-1)!/2 ciclos de Hamilton. Por exemplo, para 6 cidades necessitamos de analisar 60 ciclos. No entanto, para 25 cidades o número de ciclos a analisar é de aproximadamente 3x10²³. Mesmo que esses ciclos pudessem ser gerados à velocidade de um milhão por segundo, demoraríamos dez milhares de milhão de anos para os gerar a todos! Podemos assim dizer que, uma solução geral para este problema é pouco provável.

Se o único benefício for poupar dinheiro e tempo num plano de férias, a dificuldade de resolver problemas para grandes valores de n não nos trará grande preocupação. No entanto, o problema que temos vindo a discutir é um dos problemas mais comuns de um ramo da matemática chamado investigação operacional. É usual chamar-lhe o problema do caixeiro-viajante devido á sua primeira formulação: determinar a viagem de custo mínimo que o vendedor deve efectuar para visitar todas as cidades no seu território de vendas, começando e acabando na mesma localidade.

Existem muitas situações que requerem a solução de um problema do caixeiro-viajante: (i) um pescador de lagostas montou várias armadilhas em diversos locais e quer efectuar a recolha; (ii) a companhia de telefones quer recolher as moedas das diversas cabinas telefónicas existentes; (iii) um robô que efectua furos numa série de placas deverá estabelecer uma ordem predeterminadas. O significado do custo varia de problema para problema. Podemos medir esse custo em termos de tempo, distância, custo de gasolina, ou em termos de qualquer outro factor que possa ser optimizado.

Muitas vezes, o problema do caixeiro-viajante aparece como um subproblema de um problema mais complicado. Por exemplo, uma cadeia de supermercados pode ter um número muito elevado de lojas para ser abastecidas de um único armazém central. Se existirem menos camiãos que lojas, as lojas devem ser agrupadas por forma a que cada camião abasteça um determinado grupo. Se agora resolvermos um problema do caixeiro-viajante para cada camião, poderemos minimizar as despesas da cadeia de supermercados.

Visto que o problema do caixeiro-viajante aparece em muitas situações onde o grafo completo seria muito grande, temos que encontrar um método melhor que o método de "força bruta" que acabámos de descrever. Teremos que olhar para o nosso problema original na Figura 11 e tentar encontrar um algoritmo alternativo para o resolver. Recordemos que o nosso objectivo é o de encontrar um ciclo de Hamilton de custo mínimo.

Experimentemos uma nova alternativa: Partindo de Coimbra, visitemos primeiro a cidade mais próxima, depois visitemos a cidade mais próxima que ainda não foi visitada. Regressaremos à cidade de partida quando já não possuirmos mais nenhuma escolha possível. Este algoritmo é conhecido como o algoritmo do vizinho mais próximo. Aplicando este algoritmo à situação concreta da Figura 11, chegamos facilmente ao percurso Coimbra, Viana do Castelo, Lisboa, Évora, Coimbra, com o comprimento de 979 quilómetros.

O algoritmo do vizinho mais próximo é um exemplo de um algoritmo "avarento", visto que em cada etapa escolhe a melhor escolha (a que lhe permite poupar mais), baseada num critério apropriado. Infelizmente, como vimos anteriormente, este não é o circuito óptimo. Efectuando a melhor escolha em cada situação poderemos não ser conduzidos à melhor solução global. No entanto, mesmo para problemas do caixeiro-viajante de grandes dimensões poderemos encontrar a opção dada pelo algoritmo do vizinho mais próximo rapidamente.

Outra heurística "avarenta" é definida pelo chamado algoritmo das arestas ordenadas. Este algoritmo é definido como se segue. Depois de ordenar as arestas por ordem crescente de custo, escolher, em cada passo, a aresta de custo mínimo que: (i) não obrigue a que três arestas se encontrem num vértice; (ii) não feche um ciclo que não inclua todas as arestas. A solução obtida por este algoritmo é: Coimbra, Lisboa, Évora, Viana do Castelo, Coimbra, com o comprimento de 973 quilómetros. Assim, temos que este algoritmo, por acaso, nos deu a solução óptima.

Apesar de muitos métodos "rápidos e sujos" terem sido sugeridos para resolver o problema do caixeiro-viajante e apesar de alguns deles poderem pontualmente atingir a solução óptima, nenhum desses métodos garante a optimalidade da solução. Surpreendentemente, a maioria dos especialistas acredita que não é possível obter um método eficiente que garanta a optimalidade da solução. Estes problmas são chamados problemas NP.

3. Bibliografia (UCMA)

[1] B. Bollobás, Modern Graph Theory, GTM 184, Springer, 1998. Cota: 05C/BOL/ex.1

[2] D. Cardoso, Tópicos sobre Redes e Grafos, Universidade de Aveiro, 2001.

[3] COMAP, For All Pratical Purposes; Introduction to Contemporary Mathematics, Freeman and Co, New York, 1988. Cota: 00A06/FOR

[4] Marshall, Applied Graph Theory, Wiley, Toronto, 1971. Cota: 05C/MAR

[5] Ore, Graphs and Their Uses, Math. Assoc. America, 1990. Cota: 05-01/ORE

[6] Wilson, Introduction to Graph Theory, Logman, London, 1972. Cota: 05-01/WIL

Nota final

A primeira parte desta apresentação foi convertida numa palestra destinada a alunos do segundo e terceiro ciclo do ensino básico que pode ser ser vista aqui.