Eclipses - Eclipses Lunares
O cálculo de Eclipses Lunares segue um princípio análogo ao do cálculo de Eclipses Solares, sendo porém muito mais simples. Este cálculo pode ser simplificado dado que o tempo e as circunstâncias locais são as mesmas em todos os lugares da Terra onde a Lua é visível.
Existem três tipos de Eclipses Lunares distintos:
Eclipse Lunar Penumbral;
Eclipse Lunar Parcial;
Eclipse Lunar Total.
Esquematicamente tem-se (desloque o ponteiro do rato sobre o texto e click no desejado):
Seja: P: Paralaxe Equatorial Horizontal do Sol;
P1: Paralaxe Equatorial Horizontal da Lua;
S: Semi-diâmetro angular do Sol;
S1: Semi-diâmetro angular da Lua;
r: Distância Geocêntrica do Sol;
r1: Distância Geocêntrica da Lua;
Considere-se o seguinte esquema:

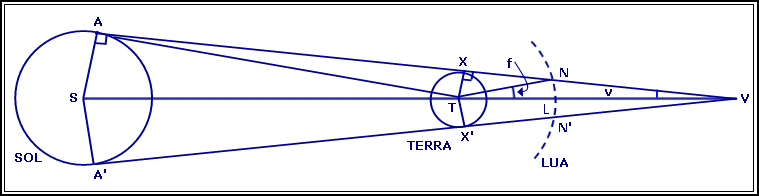
Fig. 01: Tangentes comuns ao Sol e à Terra
Nesta figura AXV e A'X'V representam duas rectas tangentes mutuamente ao Sol e à Lua, onde V é o vértice do cone umbral e v=(XVT) é o semi-ângulo deste cone. O arco de círculo NLN' a tracejado deve ser considerado como porção da órbita da Lua, assim como f=NTL representa o raio angular geocêntrico do cone umbral.
O ângulo (XNT) da figura pode ser considerado como sendo a paralaxe equatorial horizontal da Lua, ou seja P1. No entanto, o ângulo (XNT) é exterior ao triângulo [TNV], donde se conclui que f=P1-v. Utilizando um raciocínio análogo para o triângulo [TAV] conclui-se facilmente que v=S-P. Combinando as duas expressões e eliminando v, tem-se f=P+P1-S. Considerando agora uma tangente interna e o vértice do cone penumbral pode-se determinar o raio angular do cone através de f'=P+P1+S.
Um factor a ter em conta é o efeito da atmosfera terrestre que provoca um aumento de cerca de dois por cento. Sendo assim as fórmulas anteriores devem ser reescritas da seguinte maneira:
f=1.02(P+P1-S)
f'=1.02(P+P1+S)
Considere-se agora a seguinte representação de uma esfera celeste geocêntrica:
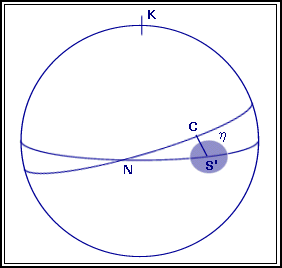
Fig. 02: Esfera Celeste Geocêntrica
Seja: K - Pólo da Eclíptica;
N - Nodo da órbita da Lua;
C - Centro da Lua;
S' - Ponto anti-solar;
h - Distância entre os pontos C e S' na Esfera Celeste;
Zona sombreada - Cone umbral à distância da Lua.
Finalmente, através das fórmulas anteriores, é possível estabelecer as condições necessárias para a ocorrência dos vários tipos de Eclipses:
| Eclipse Lunar Penumbral: | h < | 1.02(P+P1+S)+S1 |
| Eclipse Lunar Parcial: | h < | 1.02(P+P1-S)+S1 |
| Eclipse Lunar Total: | h < | 1.02(P+P1-S)-S1 |