Devido à excentricidade da sua órbita e também, com uma contribuição muito menos significativa, devido às perturbações da Lua e dos Planetas, a longitude heliocêntrica da Terra não varia uniformemente. Logo, devido a este facto e também porque o Sol se move sobre a eclíptica e não sobre o equador celeste, a sua ascensão recta não é incrementada de uma maneira uniforme.
 

    Considere-se um primeiro Sol fictício viajando ao longo da eclíptica com velocidade constante e coincidindo com o verdadeiro Sol no perigeu e apogeu (isto é, quando a Terra se encontra no periélio e afélio respectivamente). Considere-se agora um segundo Sol fictício viajando ao longo do equador celeste com velocidade constante e coincidindo com o primeiro Sol fictício nos equinócios. A este segundo Sol fictício dá-se o nome de Sol médio, e por definição a sua ascensão recta aumenta com uma taxa uniforme, isto é, não existem termos periódicos, mas a sua expressão contém pequenos termos seculares em t², t³,…

    Quando o Sol médio atravessa o meridiano do observador, dá-se o meio-dia médio, sendo que o verdadeiro acontece quando o meridiano é atravessado pelo Sol real.

    Tem-se então a Equação do Tempo definida da seguinte maneira:

E = L₀ - 0.0057183 - a + Dycose

L₀ = 280.4664567 + 360007.6982779t +0.03032028t² +

+ t³/49931 - t⁴/15300 - t⁵/2000000

    sendo:  L₀: longitude média do Sol;

               t: tempo medido em milénio julianos desde J2000.0;

               a: ascensão recta aparente do Sol (tendo em conta os efeitos da aberração e da nutação);

               Dy: nutação em longitude;

               e: obliquidade da eclíptica.

    É necessário ter em atenção que L₀, a e Dy deverão estar expressos em graus (com L₀ inferior a 360º, caso não seja, dever-se-á adicionar ou subtrair um conveniente múltiplo de 360) para que a Equação do Tempo resultar, também, em graus. No entanto é usual apresentar-se o valor para a Equação do Tempo em minutos, bastando para tal multiplicar por quatro (4) o resultado em graus.

    O valor para a Equação do Tempo poderá ser positivo ou negativo (quando dá positivo, o Sol verdadeiro atravessa o meridiano do observador antes do Sol fictício), no entanto, o seu valor em módulo terá sempre que ser inferior a vinte (20). Se o seu valor parecer ser muito grande, terá que se somar ou subtrair 24 horas.

    De seguida apresenta-se um conjunto de gráficos anuais da Equação do Tempo para os anos entre –2000 a 5000 de mil em mil anos.
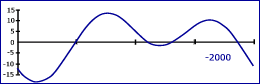
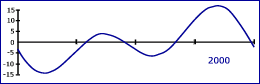
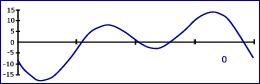
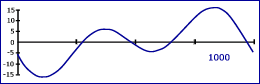