
Jornal "Expresso" de 28 de Outubro de 2000
Números no século XX: usos e abusos
Jaime Carvalho e Silva
Departamento de Matemática
Universidade de Coimbra
Se a Matemática é muitas vezes reduzida arbitrariamente à mera manipulação de números e figuras geométricas, também é verdade que os números são considerados de algum modo como parentes inferiores da matemática: elementares, frios, redutores, repetitivos e cujo domínio pela generalidade dos cidadãos até se tornará eventualmente obsoleto com o aparecimento das calculadoras e computadores!÷
Por outro lado é considerado que a Matemática tem muitas aplicações, como as relatadas em livros do tipo "Os Problemas da matemática" de Ian Stewart ou "A Experiência Matemática" de Philip J. Davis e Reuben Hersh, mas é considerado que essas aplicações apenas poderão interessar a áreas muito sofisticadas e têm pouco a ver com a vida de todos dias ou com a vida do cidadão comum.
Estas e muitas outras ideias erradas têm sido combatidas com campanhas oportunas que tentam dar à Matemática uma imagem mais compatível com a sua real importância, como aconteceu no caso do Ano Mundial da Matemática. Não se trata obviamente de ter uma ideia imperialista de que a Matemática como disciplina estaria acima das outras, que não está, mas apenas de colocar a Matemática como parte integrante de todo o conhecimento humano, seja qual seja a forma que assuma. A recusa da utilização ou até do mero conhecimento da existência (e dos limites) das ferramentas que só a Matemática pode fornecer, empobrece qualquer área do conhecimento.
Para mostrar como a Matemática é realmente uma área importante para todos vou recorrer a alguns exemplos, utilizando apenas números, e referindo apenas usos no actual século, não esquecendo alguns abusos e erros gerados por um mau domínio dos números.
O primeiro erro está reflectido de algum modo logo no título deste trabalho: ao contrário do que muita gente pensa, ainda estamos no século XX. Se é verdade que as definições de ano, século e milénio são arbitrárias e podem ser escolhidas como quisermos (podemos perfeitamente escolher dizer que um ano tem 400 dias, que um século tem 99 anos ou que um milénio tem 1500 anos, por exemplo, sem cometer nenhum erro formal), a verdade é quer, a partir do momento em que uma determinada definição é adoptada, teremos de aceitar todas as consequências lógicas que essa definição, combinada com outros elementos, nos possa trazer.
Por exemplo, numa carta publicada pelo
jornal "Público" o autor tentar demonstrar que o ano 2000 já
deve ser incluído no século XXI. Para isso "embrulha" as
contas, não se apercebendo do erro que comete, pois a ideia que
tem do lugar do ano 2000 já está definida à partida,
ou seja, os cálculos elementares que realiza não são
analisados pelo seu significado mas apenas pelo resultado pretendido, já
escolhido à partida. No fundo é a ideia de que, num problema
matemático, quando se fazem contas, o resultado obtido não
carece de análise crítica que o integre no contexto de partida,
basta obter um simples número que as pessoas logo lhe atribuem um
valor quase mágico, não carecendo de mais análises.
| "(÷) nasci no instante zero do ano
1. No final do ano de 99 eu tinha 365 dias (do ano 1, quando completei
um ano de existência) + 365*99 = 36.500 dias.
Logo 36.500:365 = 100 anos. Logo um século. No final do ano 199 eu tinha 365 dias (do ano 100 que começou às zero horas do dia 1 de Janeiro e terminou às 24h00 do dia 31 de Dezembro) + 365*199 = 73.000 dias. Logo 73.000:365 = 200 anos. Logo dois séculos." (jornal "Público" de 12.1.1999) |
Outro exemplo, este muito mais grave,
do mau domínio dos números, em particular do que se designa
por "crescimento exponencial", é o que em Portugal é normalmente
designado por D. Branca, do nome da líder da mais célebre
organização de exploração da ignorância
matemática e da ganância dos cidadãos. Este mesmo processo,
cujo esgotamento prático as pessoas não se apercebem ser
muito rápido, levou já um país inteiro à bancarrota,
a Albânia, tendo mesmo desembocado numa guerra civil que só
foi dominada com a ajuda da União Europeia.

Jornal "Expresso" de 28 de Outubro de 2000
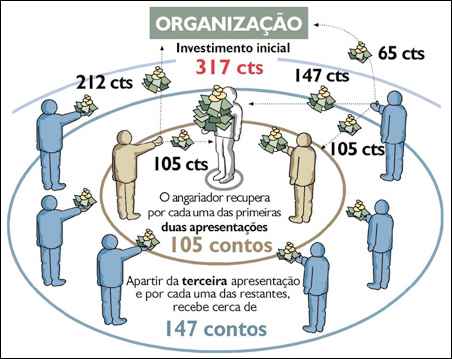
Se as pessoas fizessem certos cálculos elementares e os soubessem interpretar devidamente, observariam que um esquema como o de uma D. Branca precisa de tanta gente para funcionar que rapidamente levará à ruína da maioria daqueles que investirem as suas economias. Só não ficarão arruinados os primeiros a intervir no processo, a não ser que resolvam reinvestir os seus lucros. No caso da Albânia, o dinheiro depositado perdeu-se totalmente em especulações na bolsa internacional. A ruína nesse caso foi total. No caso de D. Branca, alguns "passarões" viveram como milionários à custa do dinheiro depositado pelos incautos.
Jornal "Expresso" de 28 de Outubro de 2000
Um pequeno cálculo com uma folha de cálculo, por exemplo, mostra facilmente que, para que os primeiros elementos tenham lucro, uma multidão de pessoas ficará com prejuízo. Mas quantas pessoas serão capazes de entender realmente um gráfico como o que o jornal "Expresso" publicou a 28 de Outubro deste ano?
Estamos constantemente a ser bombardeados com notícias que traduzem questões quantitativas sobre as quais era bom que tivéssemos uma opinião para não estarmos dependentes da opinião de especialistas que às vezes são muito pouco especializados na área de que estão a falar. E se cada cidadão conseguisse fazer por si só uma interpretação talvez o nosso comportamento como cidadãos se modificasse. Um caso paradigmático é o da relação entre as velocidades excessivas (e ilegais) nas estradas portuguesas e a poluição, um dos maiores flagelos do nosso século.
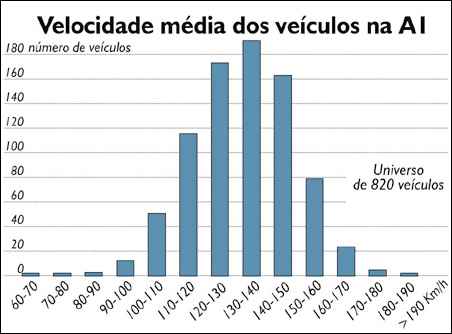
Jornal "Expresso" de 9 de Setembro de 2000
Por um lado o número de veículos com velocidades excessivas é assustador, como mostra o gráfico aqui reproduzido. Se pensarmos que o máximo legal é de 120 km/h, conseguirá a generalidade dos cidadãos fazer uma estimativa do número de veículos da amostra que circularam a uma velocidade superior ao limite legal? E conseguirão os cidadãos extrapolar daí para o universo de carros que circulam num só dia?
Mas a relação com a poluição é muito grave.

Jornal "Expresso" de 9 de Setembro de 2000
Só os números nos permitem entender que a velocidades elevadas a poluição produzida é muito maior do que a produzida a velocidades mais reduzidas. E que o aumento da poluição não é simplesmente proporcional ao aumento de velocidade, cresce mais rapidamente.
A compreensão destes números está de algum modo ligada à nossa sobrevivência no planeta Terra. Quando a poluição tornar certas zonas do planeta inabitáveis já não valerá muito a pena discutir os números÷
Podemos observar outros exemplos do
mau domínio dos números em situações que mexem
directamente com o bolso dos cidadãos. Na discussão decorrida
em 1997 de revalorização das carreiras da função
pública, foi utilizada uma certa fórmula de cálculo
que, algures, envolvia uma divisão. Claro que dificilmente o resultado
da divisão iria dar um número inteiro, mas ninguém
se apercebeu de que um resultado não inteiro não seria aceitável
pois os índices de vencimento da Função Pública
em Portugal são dados através de número inteiros.
O mais fácil foi culpar uma pobre máquina de calcular que
se limitou a dar o resultado certo com o número de casas decimais
definido nos valores de trabalho da máquina. O problema real, a
interpretação do significado do resultado de um determinado
cálculo, foi claramente ignorado, tanto pelo anónimo autor
da informação ao jornal como pelo próprio jornalista
(e pelo leitor do jornal?).
| "Máquina põe vírgulas
indevidas na Função Pública
Engano nos números do Governo (÷) Contactado pelo PÚBLICO um responsável da Secretaria de Estado reconheceu que poderia haver algum engano, já que os números apresentavam casas decimais quando tinham sido calculados com base em valores sempre absolutos. (÷) explicou que este [engano] deveria ter sido causado pela utilização de uma determinada máquina de calcular, pródiga na colocação indevida de vírgulas. (÷) Para a obtenção da revalorização (÷) e a sua divisão pelo número de escalões de cada categoria (÷) (jornal "Público" de 23.1.1998) |
Muitos utilizam o multibanco em Portugal,
como o quadro seguinte mostra sem margem para dúvidas.

Mas quantos se interrogarão se a sua utilização é realmente segura? E quantos saberão que os números primos são a chave da segurança da utilização do multibanco? E contudo não é muito difícil ter uma ideia do que se passa. Aos interessados recomendo a leitura do pequeno livro "Os números e as mensagens secretas" ů Manuel Joaquim Saraiva, Carlos Inácio Frias, Associação de Professores de Matemática, Lisboa, 1999.
Um dos desafios envolvendo números que alguns já enfrentam e todos irão enfrentar proximamente é o da mudança da nossa moeda para o EURO. Uma taxa de conversão de 200,482 escudos para 1 EURO não vai facilitar a vida a ninguém. Uma boa capacidade de fazer estimativas será essencial: por exemplo, determinar se uma aproximação de 200 escudos por cada EURO será suficiente ou se será preciso incluir alguma casa decimal.
Mas a questão não se
fica por aqui. Como o extracto de uma página de um banco encontrada
na Internet e aqui reproduzida mostra, a realização de operações
múltiplas de conversão de escudos em EURO e vice-versa levanta
outros problemas que só uma bom domínio do número
permitirá enfrentar com sucesso. E mais uma vez não vale
a pena culpar as máquinas de calcular. Elas farão bem todos
os cálculos para que forem programadas, mas não serão
capazes de interpretar os resultados e saber em que medida os erros de
arredondamento são desprezáveis ou não.
| "Questões sobre o EURO
Conversões unitárias seguidas de uma conversão inversa A conversão em escudos e, depois, em euro de uma transacção denominada originalmente em euro não cria nenhum arredondamento de conversão já que, neste caso, o escudo é uma unidade de medida mais pequena que o euro. Mas, no caso inverso, a situação altera-se. Uma dupla conversão escudo/euro/escudo pode originar um desvio que pode atingir ± 1 escudo, explicado pelo facto de um cêntimo de euro valer cerca de 2 escudos. (÷) Conversão de somas ou produtos É importante considerar que a soma dos montantes convertidos não é necessariamente igual à conversão da soma dos montantes, isto qualquer que seja o sentido da conversão. Do mesmo modo, o produto dos montantes convertidos não é igual à conversão do produto desses montantes. |
Muitos outros exemplos poderia avançar
relacionados com notícias de jornais, trabalhos de divulgação,
relatórios dirigidos ao grande público, debates na televisão,
etc.

Jornal "Expresso" de 4 de Dezembro de 1999
Concluirei este texto com um exemplo que me parece exemplar a vários títulos: a má utilização de números simples num projecto científico de grande envergadura e grande impacto público.
Como a notícia junta documenta, a agência espacial americana NASA perdeu em 1999 a nave espacial Mars Climate Orbiter por causa de uma simples confusão entre números expressos em unidades diferentes. O acumular de erros de cálculo fez com que a nave ao chegar a Marte se tivesse desviado mais de 100 km da trajectória prevista, desfazendo-se na atmosfera de Marte (a margem de segurança era de 75 km). Não só os técnicos da NASA não se aperceberam do erro ao introduzir os dados no computador para fazer os cálculos relativos ao controle dos motores, como, além do mais, não tinham elementos verificadores dos resultados obtidos: desde que partiu da Terra a nave espacial esteve sempre numa posição diferente daquela calculada pelos técnicos; numa viagem de 700 milhões de quilómetros e de vários meses a nave espacial ia ficando cada vez mais afastada da órbita necessária e ninguém se apercebeu disso!
Como preparar os cidadãos para os usos e abusos dos números no século XX e nos séculos seguintes: melhorando a Educação Matemática!