Fibonacci




Fibonacci ist einer der berühmtesten Mathematiker. Wikipedia sagt über ihn:

Leonardo da Pisa, auch Fibonacci genannt (* um 1180? in Pisa; † nach 1241? in Pisa) war Rechenmeister in Pisa und gilt als der bedeutendste Mathematiker des Mittelalters. Bekannt sind heute vor allem die nach ihm benannten Fibonacci-Zahlen.

Fibonacci

Wikipedia sagt zu der Fibonacci-Folge:

Die Fibonacci-Folge ist eine unendliche Folge von Zahlen (den Fibonacci-Zahlen), bei der sich die jeweils folgende Zahl durch Addition ihrer beiden vorherigen Zahlen ergibt: 0, 1, 1, 2, 3, 5, 8, 13, … Benannt ist sie nach Leonardo Fibonacci, der damit 1202 das Wachstum einer Kaninchenpopulation beschrieb. Die Folge war aber schon in der Antike sowohl den Griechen als auch den Indern bekannt.




Man findet diese Folge in verschiedenen mathematischen Bereichen wieder.

1)  Berühmt ist die Verknüpfung mit dem goldenen Schnitt. Genauer der goldenen Spirale:

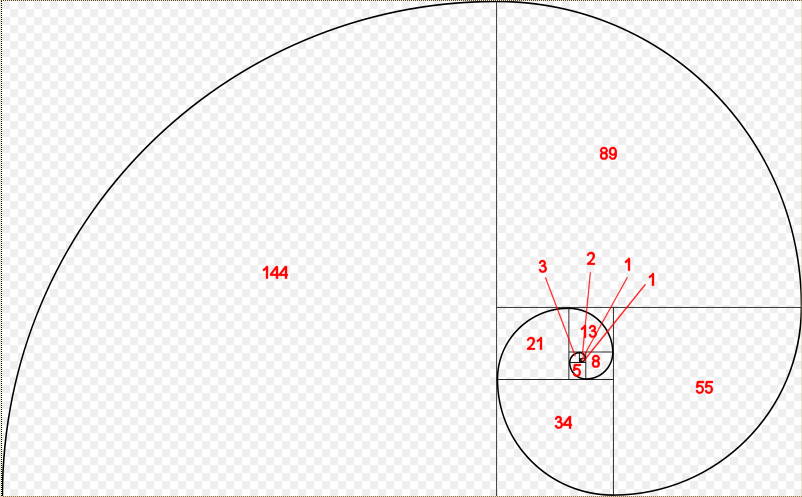
Reiht man Quadrate aneinander, welche die Seitenlänge der Zahlen der Fibonacci-Folge haben, so entsteht immer ein Rechteck, welches dem Goldenen Schnitt nahe kommt. Die längere Seite des Rechteckes ist wiederum die Seitenlänge des nächsten Quadrats, der nächsten Fibonacci-Zahl.

Verbindet man die Ecken der Quadrate, so entsteht eine Spirale. Diese Spirale wird auch als „Goldene Spirale“ bezeichnet (Fig.14)  [1]


Godene Spirale - Fibonacci-Folge
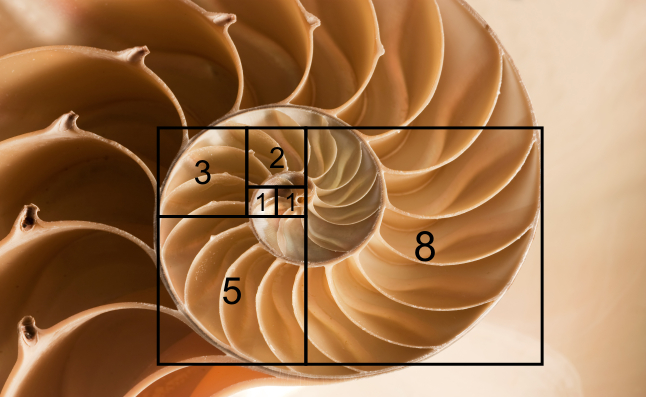
Diese ist auch in der Natur wiederzufinden. Zum Beispiel in der Form von Schneckenhäusern:

Schneckenhaus
2) Die Fibonacci-Folge findet sich auch in der Natur wieder. Hier einige Beispiele:
                        In der Anordnung der Kerne in der Blüte der Sonnenblume findet sich die Fibonacci-Folge wieder.

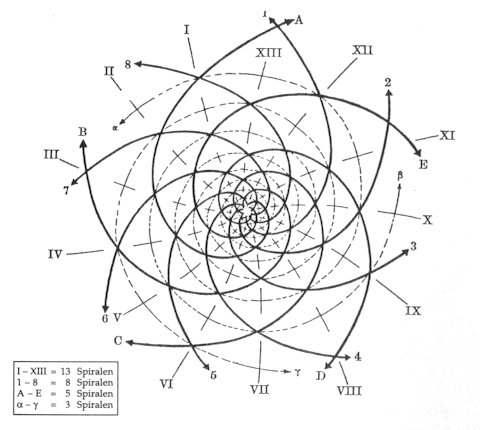
Wie viele andere Pflanzen weist die Sonnenblume im Bauplan ihres Blütenstandes Spiralen auf, deren Anzahl durch die Fibonacci-Folge gegeben ist. Das ist der Fall, weil der Winkel zwischen architektonisch benachbarten Samen bzw. Teilblüten bezüglich der Pflanzenachse der Goldene Winkel ist. Hintergrund ist der Umstand, dass die rationalen Zahlen, die den zugrunde liegenden Goldenen Schnitt am besten approximieren (annähern), Brüche von aufeinanderfolgenden Fibonacci-Zahlen sind. Die Spiralen werden daher von Pflanzenelementen gebildet, deren Platznummern sich durch die Fibonacci-Zahl im Nenner unterscheiden und damit fast in die gleiche Richtung weisen. [2]


                       Hier ein Schema:
Fibonacci Sonnenblume   dfsdf


3) Berühmt wurde die Fibonacci-Folge allerdings durch ein Planspiel über die Vermehrung von Kaninchen. Die Population der Kninchen entwickelt sich ähnlich der Fibonacci-Folge. Dabei entsprechen die Zahlen jeweils einenm Kaninchenpaar. Unter Berücksichtigung der Zeit des Heranwachsens gibt sich dann folgendes Schema:

Ein Kaninchenpaar wirft vom zweiten Monat an in jedem Monat genau ein junges Kaninchenpaar. Dieses und alle Nachkommen verhalten sich ebenso. Wieviele Kaninchenpaare sind nach einem Jahrv vorhanden, wenn kein Kaninchen stirbt oder aus dem Stall entflieht?


Kaninchen
Dieses Video beleuchtet noch einmal Beispiele der Fibonacci-Folge in der Natur:







Poesie
“

One
Small,
Precise,
Poetic,
Spiraling mixture:
Math plus poetry yields the Fib.

 ”

—Pincus, Gregory K.[1]

Say
how
can I
remember
your love for me now
When you are lost and gone away forever.


A
Fib
Poem:
Not a lie,
but a math poem.
A gift from Fibonacci's mind.


Sun
shines
down but
I can't go
outside to play cause
I have to do my work. Dammit.