The equiangular spiral
As far as the animal that lives in a shell grows it needs the shell to grow in the same proportion, in order to continue to live inside it.
When shells grow they keep always the same shape. This growth process yields an elegant spiral structure (very visible when the
shell is sliced). The widths of the straight lines that link
the shell center (the spiral origin) to the points of the shell increase, but the amplitudes of the angles defined by those
lines and the corresponding tangents to the shell are constant, that is, shells follow an equiangular spiral.
This fact was identified in the 17th century by Christopher Wren.
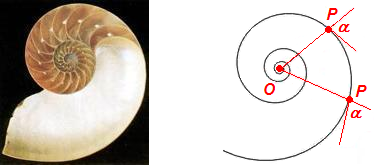
Given a point O (the origin or the pole of the spiral), the equiangular spiral follows the rule that, in each of its points P,
the amplitude of the angle 
defined by its tangent and
the line OP is constant:
Jacob Bernoulli (1654-1705) called it the Spira mirabilis (wonder spiral). It was first described mathematically in 1638 by René Descartes (who believed that "only mathematics is certain, so everything must be based on mathematics"). Its equation is given, in terms of polar coordinates r and
, by )=A e cot
where A is the radius associated to
=0. It gives the distance of
a curve point to origin O in terms of . Equivalently, the equation may be given by
log(r/A)= cot. By that reason, the equiangular spiral
is also known as the logarithmic spiral.
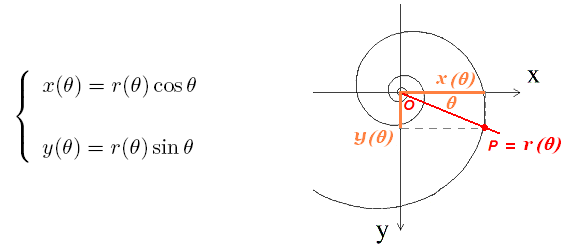
In cartesian coordinates, the points (x(
), y( )) of the spiral are given by
Note that when
=90o, the equiangular spiral degenerates to a circle.
Of course the animal would not be very satisfied with a circular shell, because he could not keep growing inside the shell.
If is not a right angle, then a true spiral forms, which corresponds to an enlargement of the shell.
This growth process keeps the shape of the shell and is called gnomonic. In geometry, the gnomon (a word of greek origin, due to Aristotle) of a given picture is a second picture that, added or subtracted to the former, generates a third picture similar to the original one. This growth pattern is so common that it is referred by many as a "law of nature". The majority of animal horns and nails, corals and snails, among other examples, also follow, basically, equiangular spirals.
