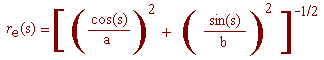The basic model
«The surface of any shell may be generated by the revolution about a fixed axis
of a closed curve, which, remaining always geometrically similar to itself, increases its dimension continually. [...] Let
us imagine some characteristic point within this closed curve, such as its centre of gravity. Starting from a fixed
origin, this characteristic point describes an equiangular spiral in space about a fixed axis (namely the
axis of the shell), with or without a simultaneous movement of translation along the axis. The scale of the figure increases in geometrical
progression while the angle of rotation increases in arithmetical, and the centre of similitude remains fixed. [...]
The form of the generating curve is seldom open to easy mathematical expressions.»
D'Arcy Thompson [5, Chapter XI]
A simple model for the growth of Mollusk Shells
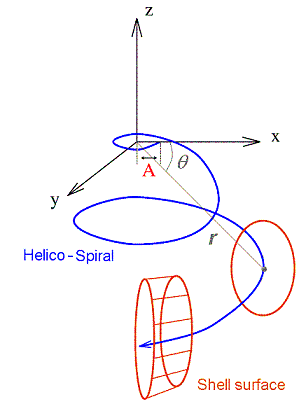
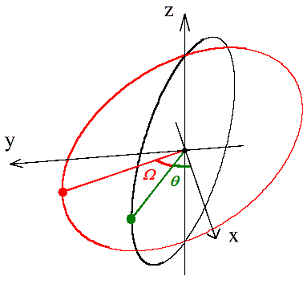
First, fix a three-dimensional cartesian system of coordinates XYZ and consider the parametric equation of an helico-spiral, written in polar coordinates r and
:
Let
- alpha: equiangular angle of spiral H
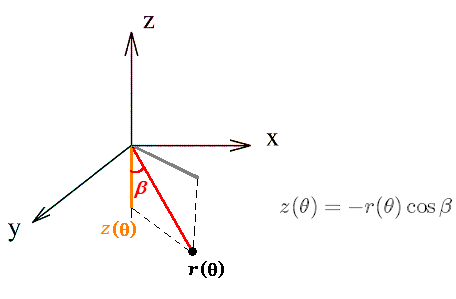
- beta: angle between Z-axis and line from aperture local origin to XYZ origin
-
A: size of the spiral aperture (distance from main origin
of aperture at =0).
) of the corresponding point
(x(), y(), z())
of H to the origin is given by
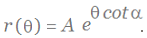
and
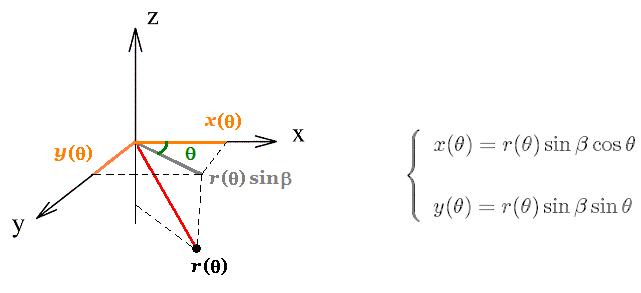
Therefore, the points (x,y,z) of the helico-spiral satisfy equations
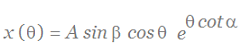
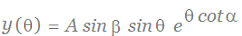
The generating curve that determines the surface of the shell is, in most cases, an ellipse with parameters
- a: half length of the major axis of ellipse (at the origin),
- b: half length of the minor axis of ellipse (at the origin),
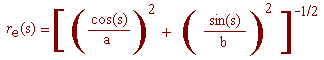
The width of C increases as far as it moves along H. We assume that its increasing rate ri(
) is the same as the one of H, that is,
ri()=
. Then, the equation of each C in
polar coordinates (centered at the corresponding H() is given by
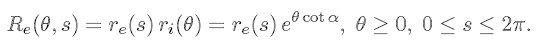
Equivalently, in terms of cartesian coordinates:
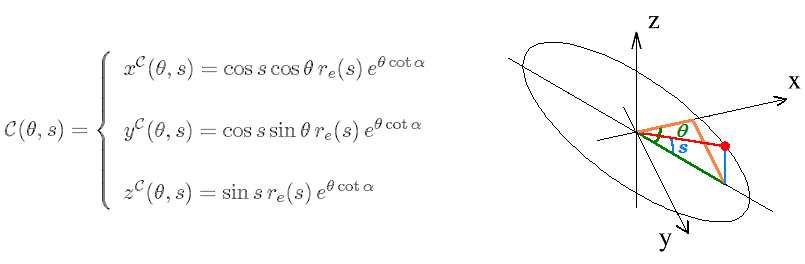
Finally, to obtain the equation of the shell, it suffices to put the equations of C in the corresponding points of H:
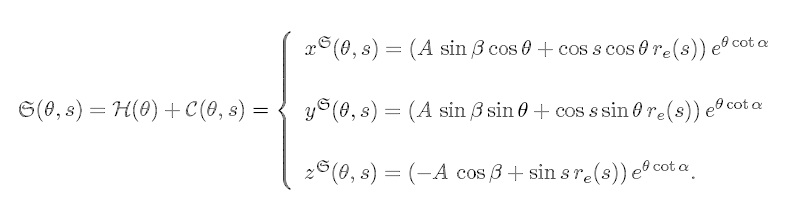
We can now easily extend this model to the more general situation where the generating
ellipse C rotates in space. For this
we specify three angles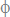 
, 
, 
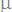, that establish the orientation
of the generating curve in space. They measure the rotation of the curve around, respectively, a vector orthogonal to the plane of the ellipse,
the OZ axis and its major axis:
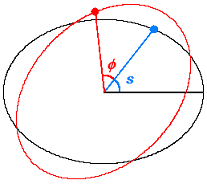
Case 1 (rotation
): it suffices to replace s by s +
in each sin and cos function in the equations
of the points of C.
Case 2 (rotation
): it suffices to replace
by + in each sin and cos function in in the equations
of the points of C.
Thus, the equations of C above are replaced by
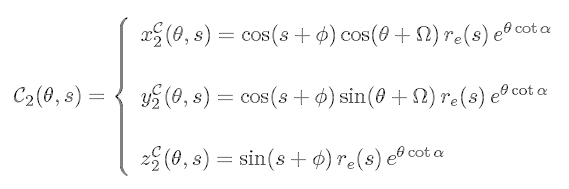
that is, the equations of the shell are now given by
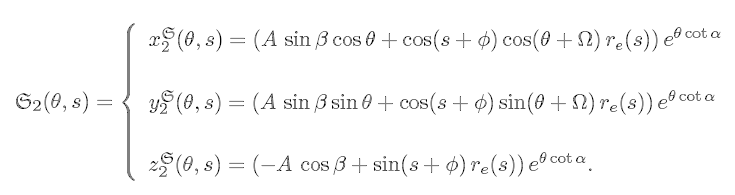
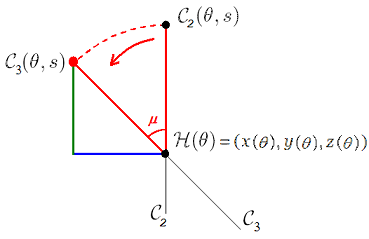
Case 3 (rotation 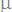): Observing the ellipse C2 by profile and the result of its
rotation of angle 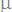, let
C3(,s)=(x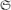3
(,s),
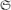y3(,s),
z3(,s)) be the
point on the new ellipse C3 corresponding
to C2(, s):
Then
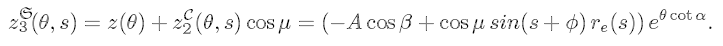
Further, looking from above we have
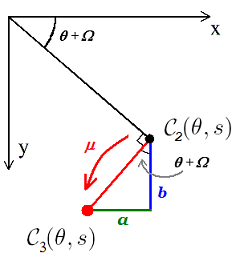
from which we conclude that
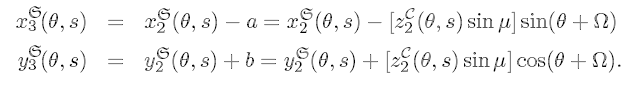
Conclusion:
Based on the above description, the parametric equations that describe the shell surface are given by
-
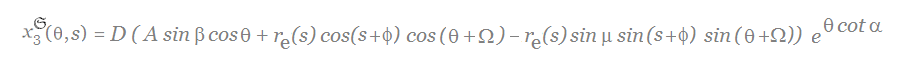
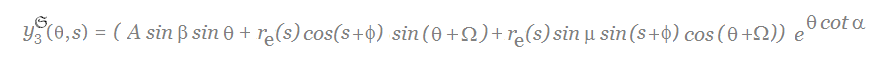
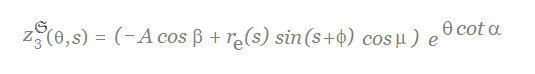
D: direction of coiling (1=dextral, -1=sinistral)
