(o seu comprimento chama-se velocidade de f no ponto f(t)).
Note que a velocidade da curva não é constante; portanto, f não está parametrizada por comprimento de arco:
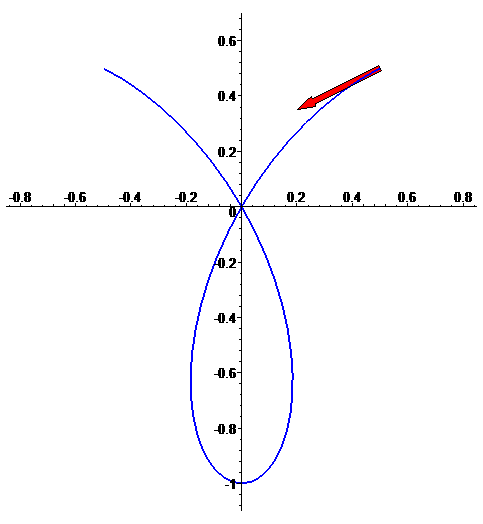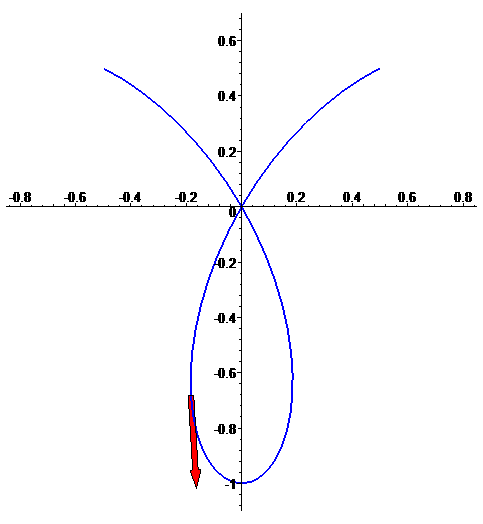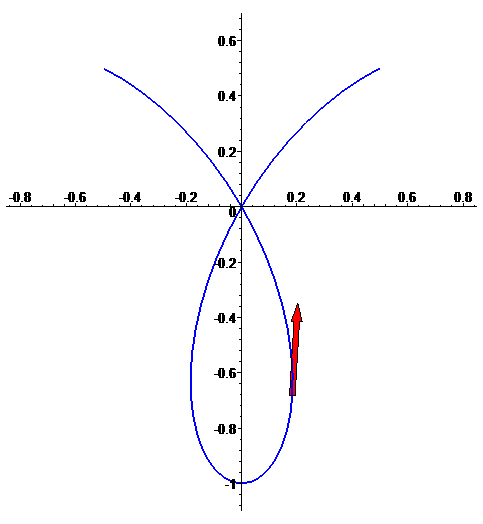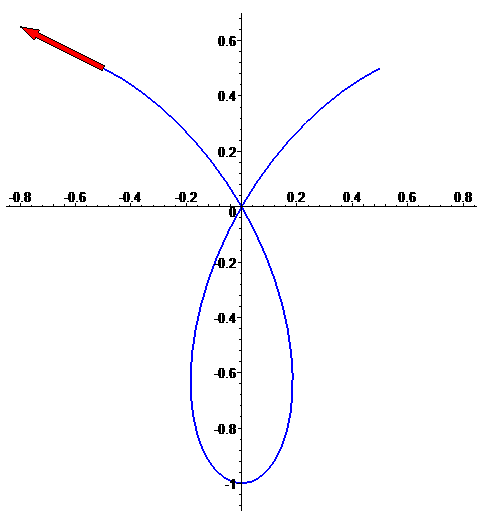
Curva plana
f: t --> [sin(3t)cos(t), sin(3t)sin(t)],
com t em [Pi/4,3 Pi/4]
Vector tangente (ou vector velocidade) f'(t)
(o seu comprimento chama-se velocidade de f
no ponto f(t)).
Note que
a velocidade da curva não é constante;
portanto, f não está parametrizada por comprimento de arco:

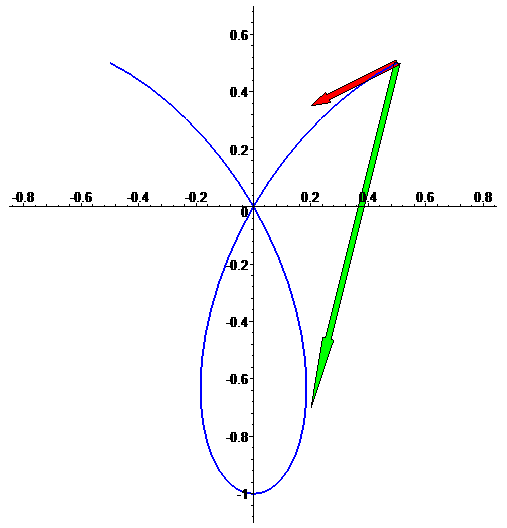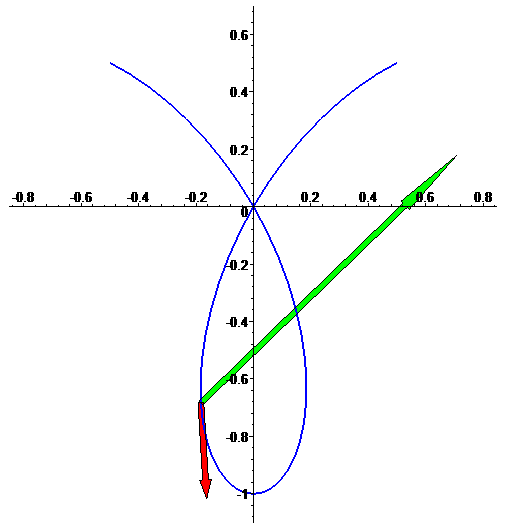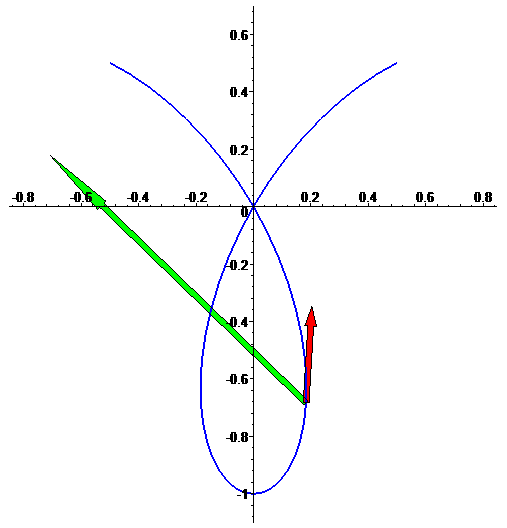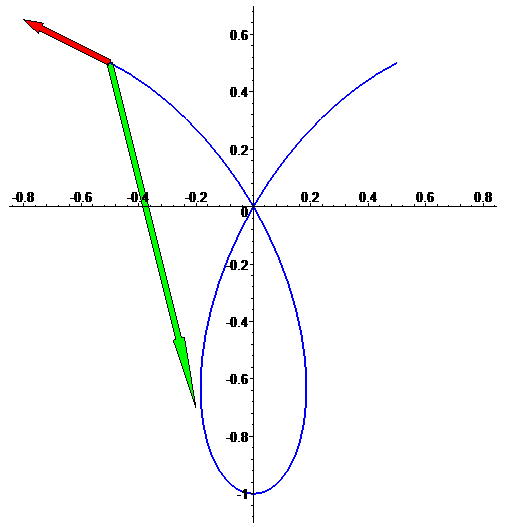
Vector tangente f'(t) e vector aceleração f''(t)
(note que nem sempre são ortogonais entre si; isso acontece porque
f não está parametrizada por comprimento de arco):
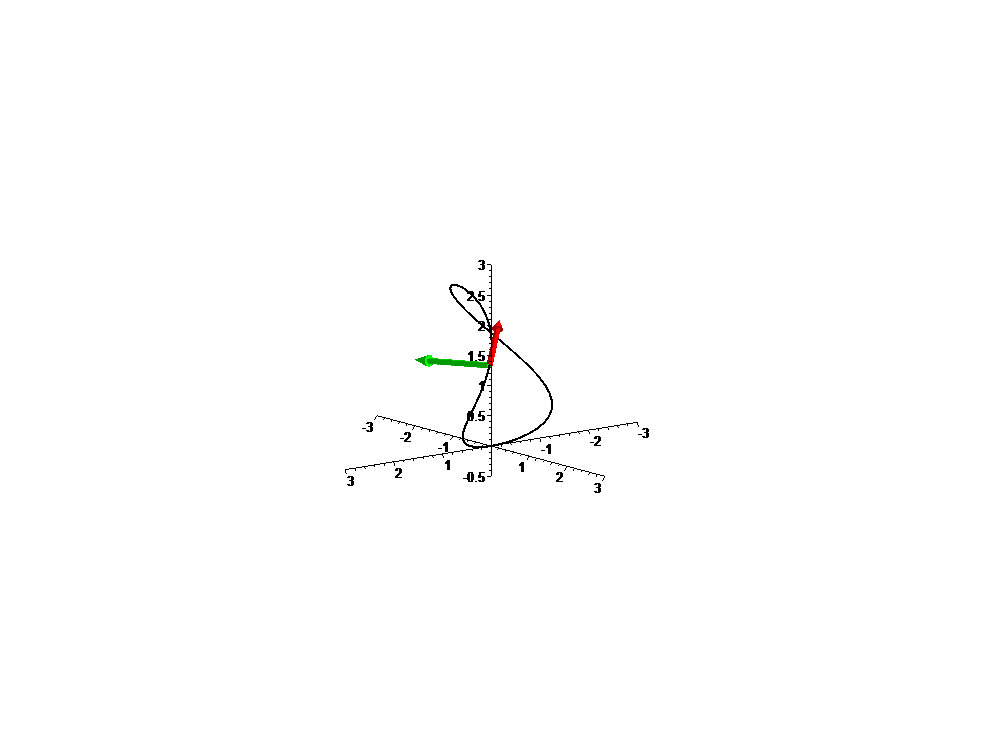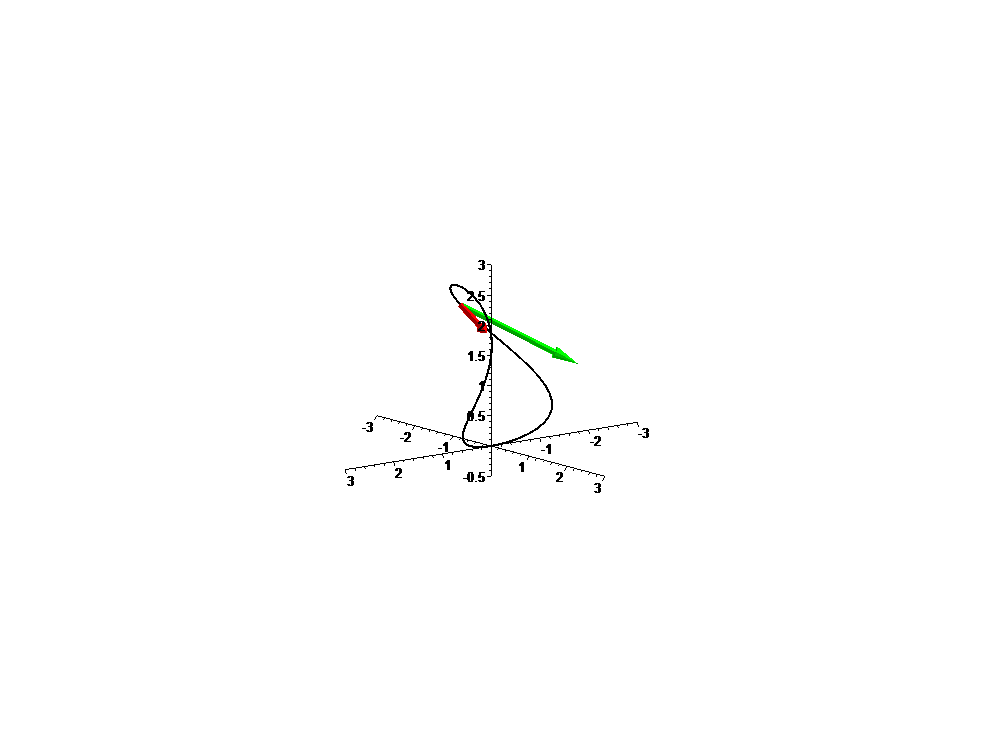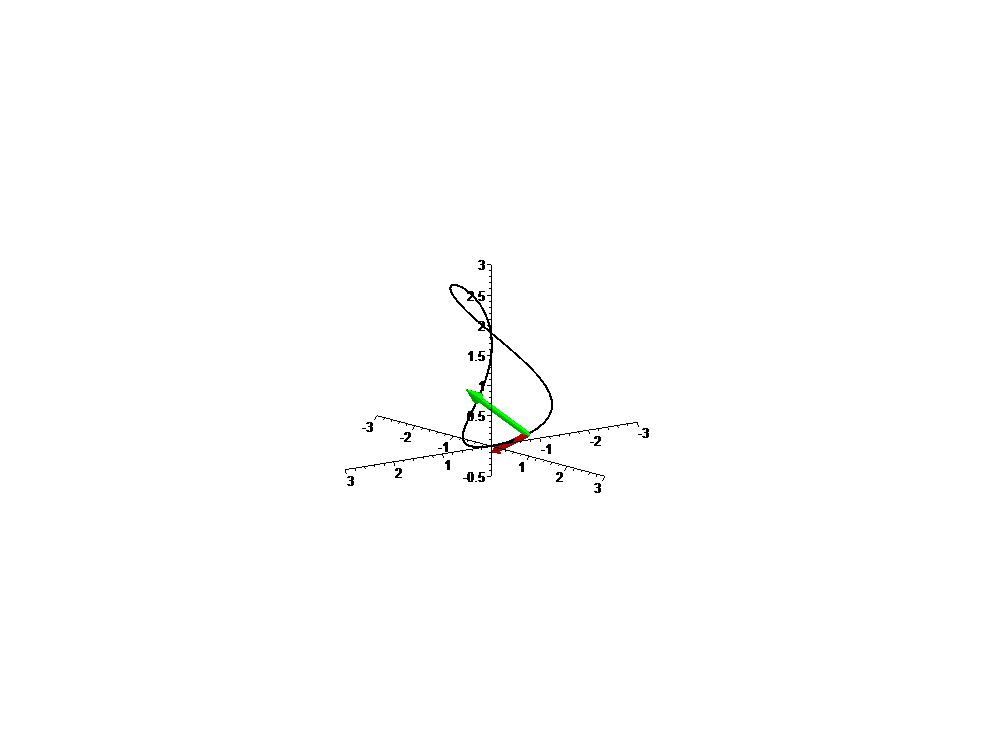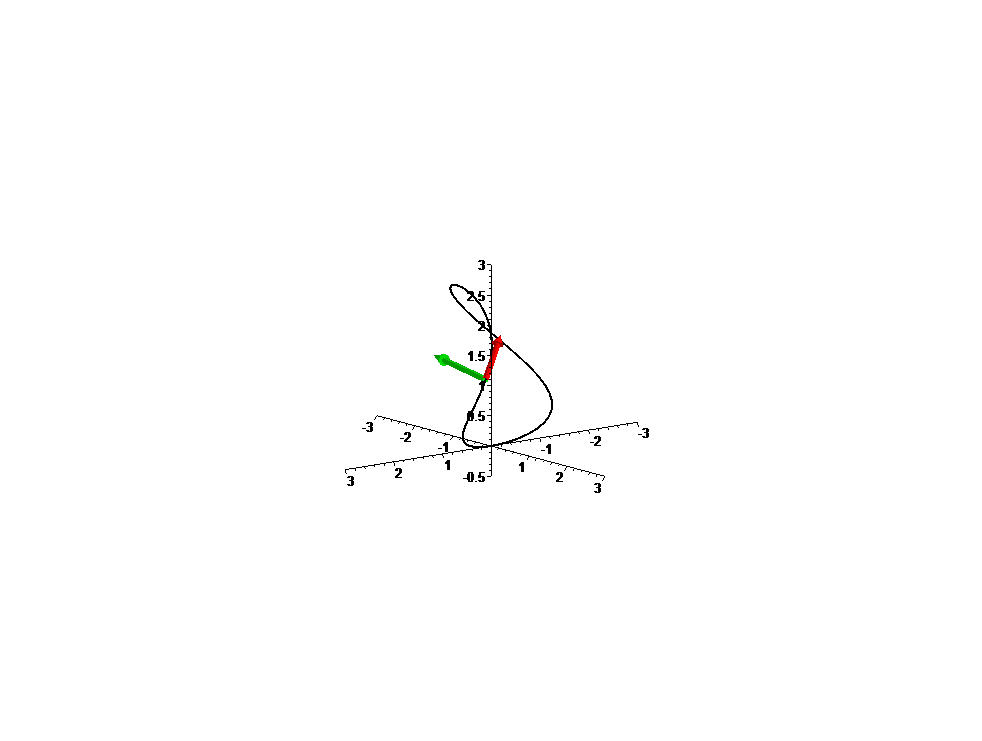
Curva
f: t --> [sin(3t)cos(t), sin(3t)sin(t), 2.5 sin(t)^2], com t em [Pi/4,5 Pi/4]
Vector tangente f'(t) e vector aceleração f''(t).
Note que
a velocidade da curva não é constante;
portanto, f não está parametrizada por comprimento de arco:
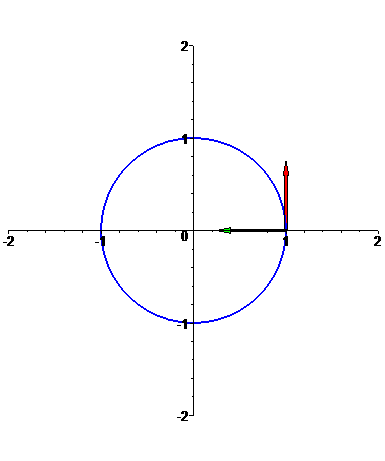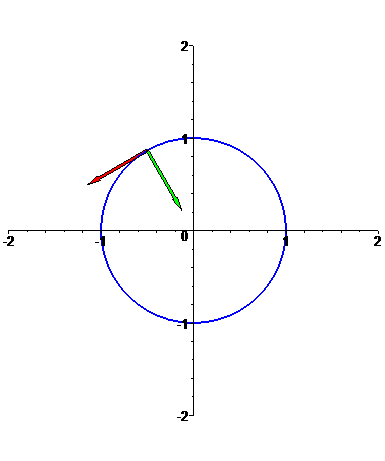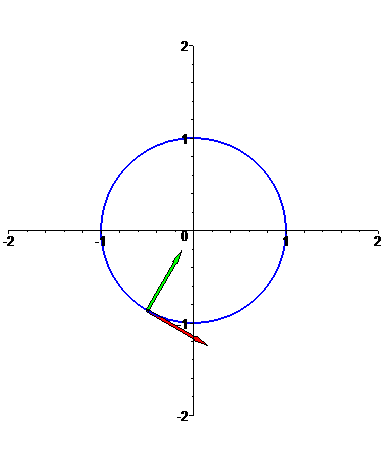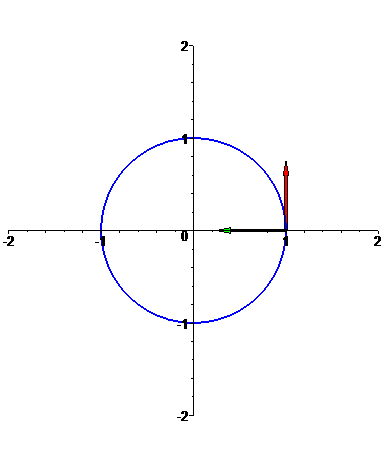
Circunferência
f: t --> [cos(t),sin(t)],
com t em [0,2 Pi].
Note que
a velocidade da curva é constante, igual a 1;
portanto, f está parametrizada por comprimento de arco e, consequentemente, os vectores f'(t) e
f''(t) são ortogonais em qualquer ponto da curva:
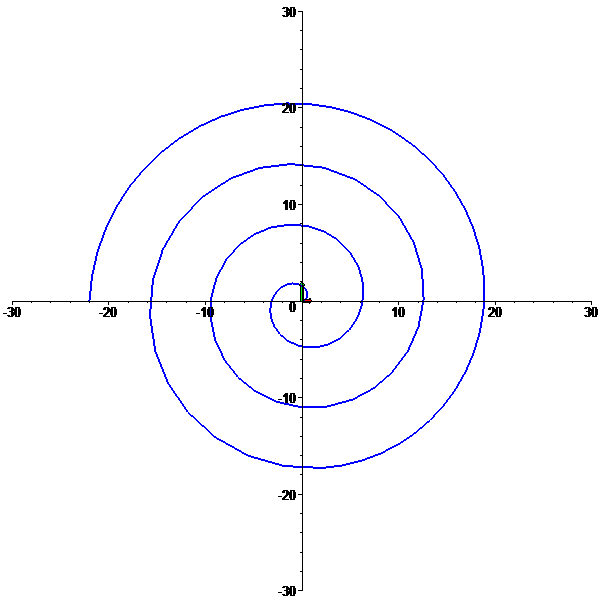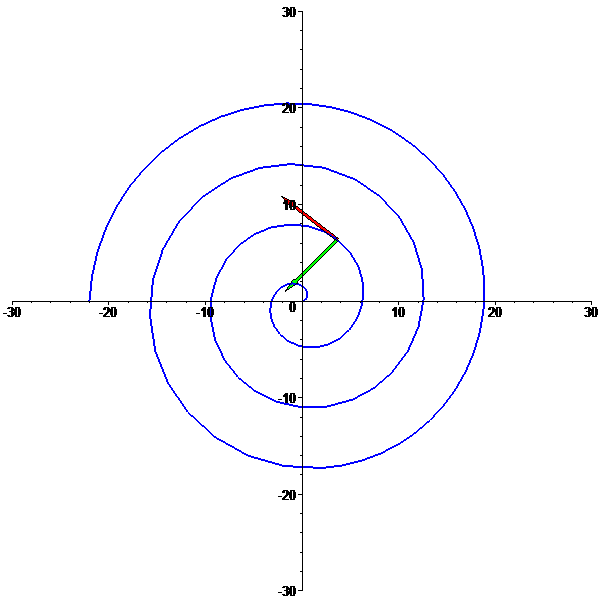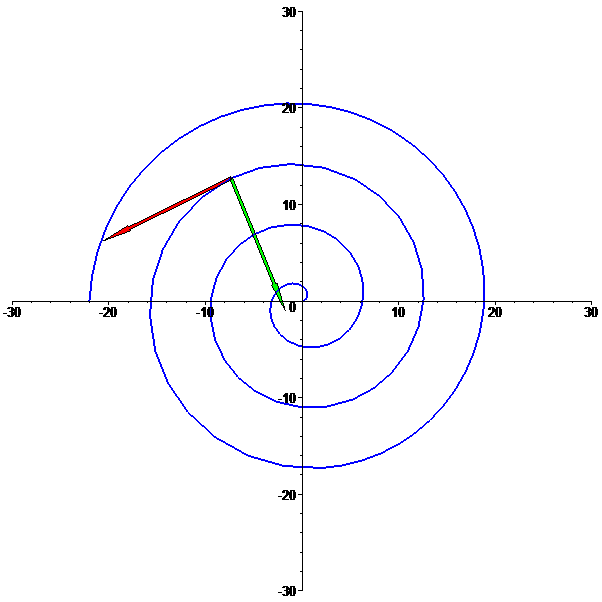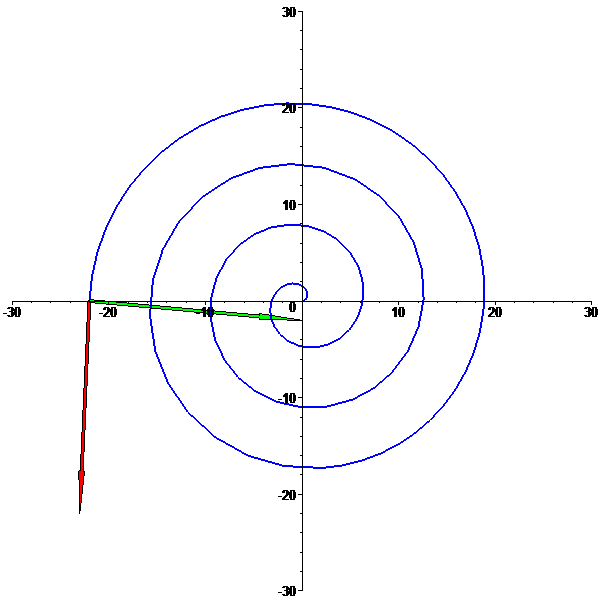
Espiral logarítmica
f: t --> [t cos(t),t sin(t)],
com t em [0,7 Pi]:
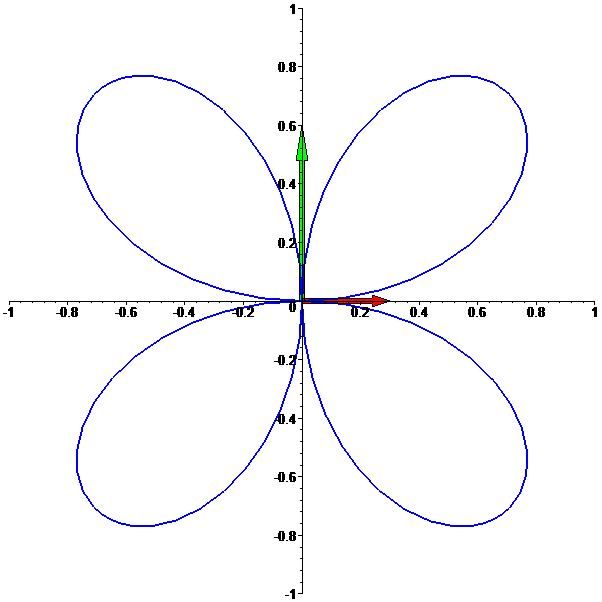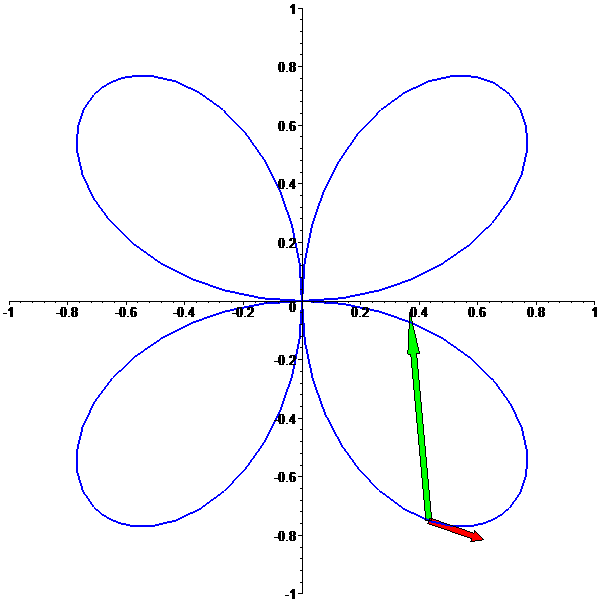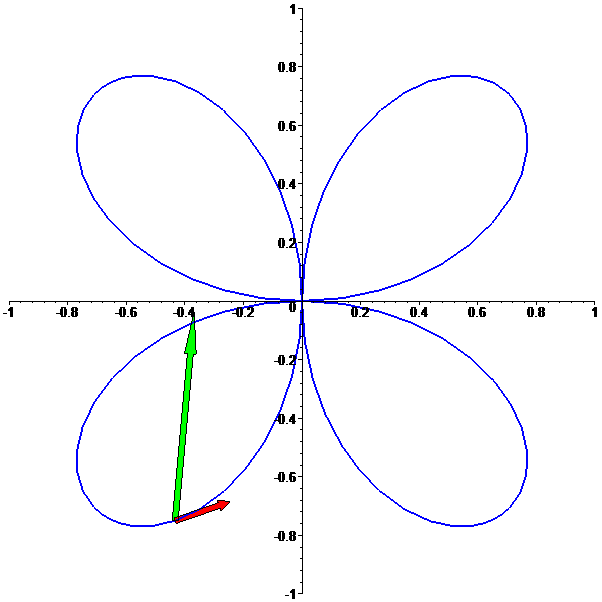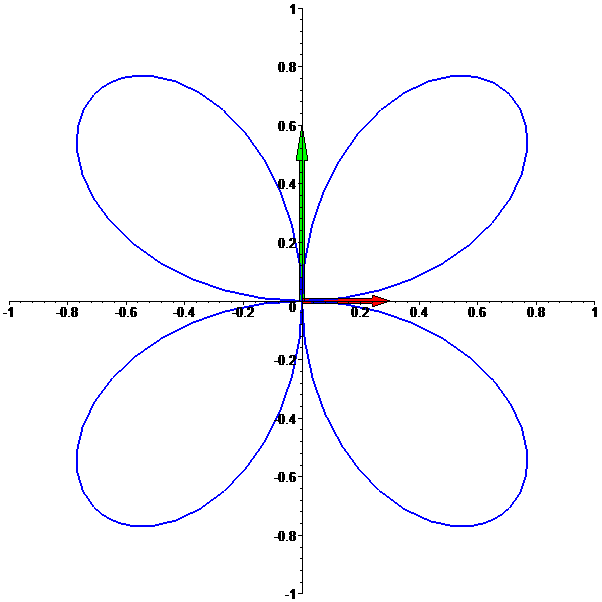
Trevo
f: t --> [sin(2t)cos(t),sin(2t)sin(t)],
com t em [0,2 Pi]:
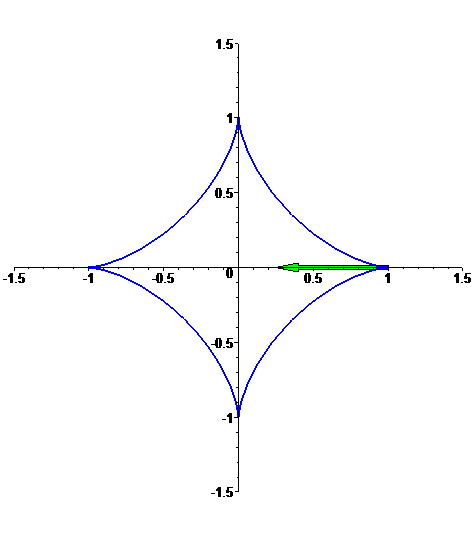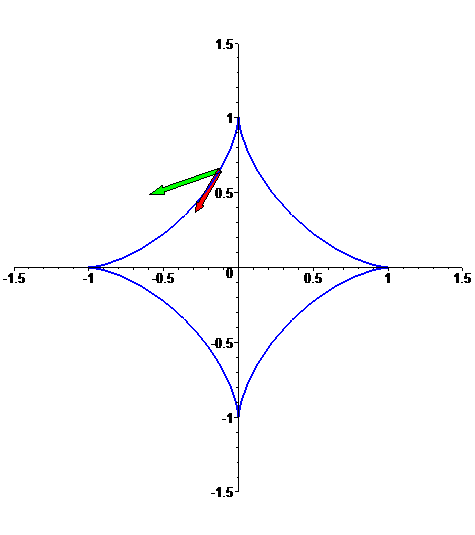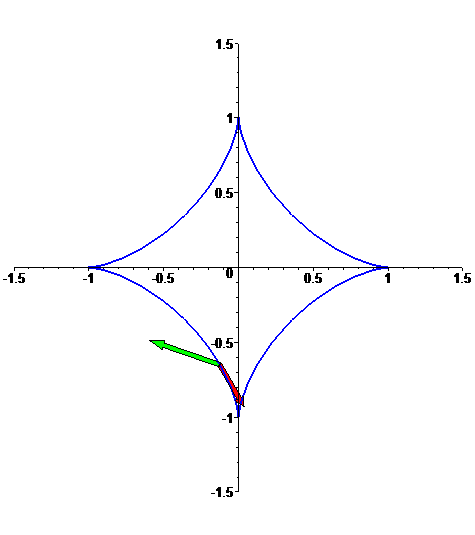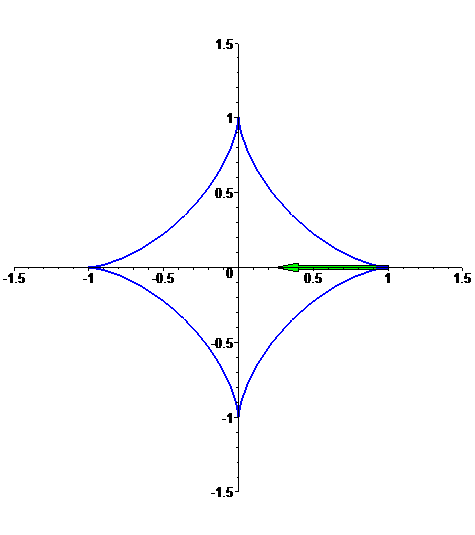
Astróide
f: t --> [cos^3(t),sin^3(t)],
com t em [0,2 Pi]:
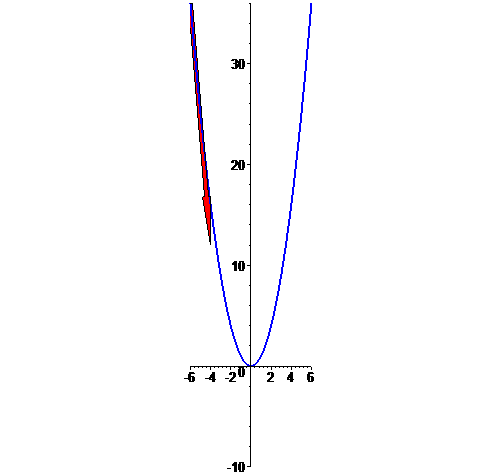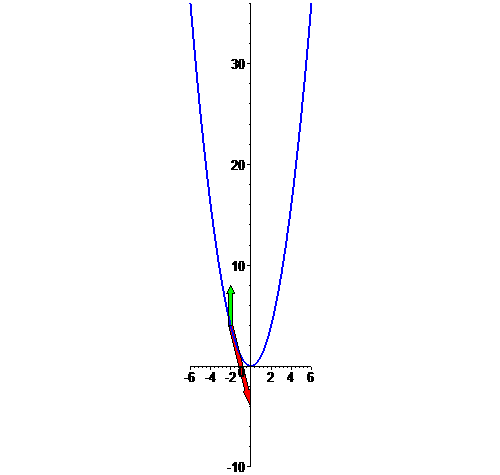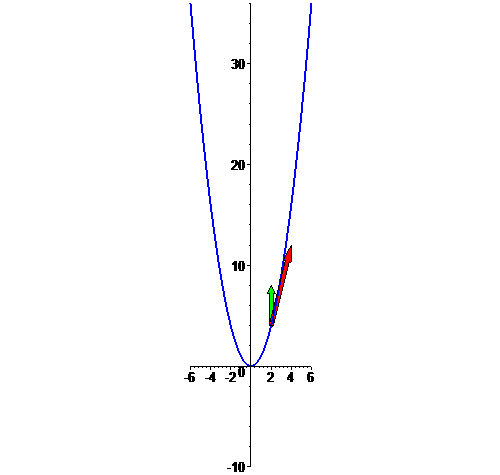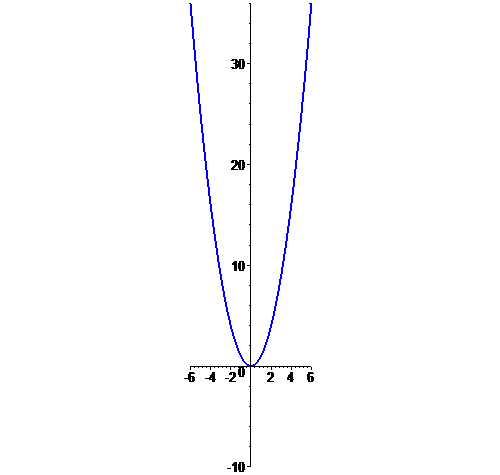
Parábola
f: t --> [t,t^2],
com t em [-6,6]: