1. BREVE APRESENTAÇÃO DO PROGRAMA

Os fractais são figuras caracterizadas pela propriedade de auto-semelhança: uma parte dessas figuras reproduz, exacta ou aproximadamente, a totalidade.

O programa FRACTAIS permite desenhar no ecrã de um computador o famoso conjunto de Mandelbrot (ou uma ampliação, "zoom", de parte dele), ou um qualquer dos conjuntos de Julia que estão associados aos pontos do conjunto de Mandelbrot (também são possíveis "zooms" dos conjuntos de Julia). Os conjuntos de Mandelbrot e de Julia são auto-semelhantes.

Figuras desse tipo, que são geradas com base em procedimentos recursivos simples, têm um grande poder de atracção estética. Os conjuntos de Mandelbrot e de Julia mostram como a matemática pode estar próxima da arte...

A matemática necessária para a produção das imagens resume-se a uma fórmula iterativa no plano dos números complexos z = x + i y :

z_n+1 = z_n + c ,

com c=a+ib uma constante complexa e n=0,1,2,.... Tem de se partir de um certo valor de z₀ ("semente"). O conjunto de Mandelbrot é o conjunto dos valores de c tais que, para z₀ = 0, a iteração não diverge, isto é, z não toma valores arbitrariamente grandes. Um conjunto de Julia, por outro lado, associa-se a cada número c do conjunto de Julia: é o conjunto das "sementes" z₀ para as quais a iteração não diverge. Os textos de apoio, no fim deste manual, fornecem explicações adicionais.

Embora o tema dos fractais não faça ainda parte dos currículos do ensino secundário (mesmo no ensino superior o seu ensino é, por enquanto, apenas pontual), pensam os autores de FRACTAIS que a simplicidade da matemática de base e a sedução das imagens produzidas podem ajudar ao desenvolvimento do interesse dos alunos pela matemática, no quadro, por exemplo, de actividades extra-curriculares.

2. CARACTERÍSTICAS TÉCNICAS

Equipamento necessário

O programa, que corre num computador pessoal PC compatível IBM, com placa gráfica VGA ou EGA (640x 480), beneficia bastante da presença de uma placa VGA. O programa beneficia de um processador rápido (Intel 386, 486 ou compatível com estes) e de um coprocessador matemático (387, 487). Num computador do tipo AT (com processador 286) o tempo de produção das imagens é demasiado longo, sendo o programa quase impraticável.

O programa exige um rato ("mouse").

A versão apresentada, programada com o compilador Turbo C, da Borland Internacional, requer os seguintes ficheiros, indicados com a respectiva extensão:

Ficheiros Principais

FRACTAIS.EXE

Ficheiros Auxiliares

JULIA.DEM

JULIA. nº (1,2,3, etc)

MAND. nº (1, 2, 3, etc)

INTRO.PCX

JULIA.PCX

MAND.PCX

MENU.PCX

VERF.PCX

FRACTAIS.TXT (texto do manual em ASCII)

Instruções Gerais

Recomenda-se que o utente efectue uma cópia de salvaguarda da disquete com o programa.

Pode correr o programa directamente da disquete ou copiá-lo para uma directoria do disco duro. Recomenda-se este último procedimento.

Se o cursor estiver posicionado na disquete (A: ou B:) tecle FRACTAIS, premindo de seguida a tecla «Enter». Se tiver copiado o conteúdo da disquete para o disco duro, posicione-se na directoria onde está o programa, tecle FRACTAIS e «Enter».

Depois de um écran de apresentação, que se manterá durante alguns segundos (premindo qualquer tecla avança-se imediatamente), aparece o menu principal, com o aspecto apresentado na Fig.1

3. COMO FUNCIONA O PROGRAMA

O menu principal (Fig.2), que aparece depois da imagem inicial, permite efectuar uma escolha entre:

- Mandelbrot (construção do conjunto de Mandelbrot).

- Ver Fractais (visualização de imagens produzidas).

- Julia (construção de conjuntos de Julia).

A selecção é efectuada por meio de pressão no botão esquerdo do rato quando o cursor deste está sobre o rectângulo conveniente.

No menu principal, pode abandonar-se o programa, voltando ao sistema operativo, clicando com o rato no pequeno quadrado do canto superior esquerdo do ecrã.

Na primeira opção (Mandelbrot) aparece o ecrã representado na Fig. 3. Com o auxílio do rato, escolhe-se no quadro da direita o nome (número) do ficheiro que vai conter a imagem a criar.

Escolha no quadro inferior o ponto (x,y) do plano complexo que serve de vértice superior esquerdo ao quadro da imagem, assim como o tamanho da janela (Dx = Dy) e a resolução (R).

O programa sugere valores para (x,y), para Dx = Dy. As partes real e imaginária dos números complexos aparecem multiplicadas por um factor de 100. Alguma experimentação permite descobrir valores adequados para obter um certo efeito. Escolhe-se ainda a resolução que se pretende para a imagem: a resolução 1 é a melhor, mas as imagens com essa resolução demoram mais tempo a criar (num computador lento, convém escolher uma resolução 2 ou 3, ficando nessa altura o utilizador apenas com uma visão "desfocada" da imagem).

Um clique com o rato quando o respectivo cursor se encontra sobre o quadro da imagem é suficiente para iniciar o processo de iteração e fazer aparecer o conjunto de Mandelbrot. Um clique com o botão direito do rato permite interromper o processo de iteração em qualquer altura. Nessa altura, pode regressar-se ao menu principal carregando com o rato no quadrado do canto superior esquerdo. Para continuar o processo de iteração se pretende um "zoom" de uma imagem, carregue com o rato no botão de "zoom". Deve em seguida escolher-se o canto superior esquerdo do quadrado que se pretende ampliar, clicando com o botão esquerdo do rato, e o canto superior direito, clicando com o botão direito do rato. Em seguida clique no interior do quadrado pequeno. São permitidos "zooms" sucessivos, embora exista um limite para o número total dessas ampliações. A saída para o menu principal faz-se clicando no quadrado do canto superior esquerdo.

Na terceira escolha do menu principal (Julia), aparece no quadro do lado direito o conjunto de Mandelbrot (Fig. 4). Deve começar-se por escrever o nome (número) do ficheiro de saída. Um clique do rato quando o cursor está sobre o quadro do conjunto de Mandelbrot permite "navegar" no plano complexo, isto é, percorrer os pontos c=(a,b) necessários para a construção dos conjuntos de Julia. Um clique com o rato num certo sítio permite escolher um dado valor de c, que aparece indicado por cima do quadro da direita. De seguida, deve escolher-se o ponto (x,y) que define o canto superior esquerdo do quadro do conjunto de Julia, assim como o intervalo Dx = Dy e a resolução da imagem. São fornecidos valores por "defeito". Finalmente, um clique no interior do quadro da esquerda faz iniciar a construção do conjunto de Julia. Para interromper os cálculos, deve carregar-se no botão direito do rato. Tal como no caso do conjunto de Mandelbrot, são permitidos "zooms" do conjunto de Julia: o procedimento é o mesmo. A saída para o menu principal faz-se por clique no quadrado do canto superior esquerdo.

A segunda escolha do menu principal serve para visualizar imagens de conjuntos de Mandelbrot e de Julia em arquivo na disquete ou no disco duro. O quadro da direita destina-se a mostrar conjuntos de Mandelbrot, enquanto o quadro da esquerda se destina a mostrar conjuntos de Julia (Fig. 5). Para seleccionar um dado ficheiro basta, com a ajuda do rato, obter o respectivo número em baixo. Um clique dentro de cada um dos quadros provoca a afixação de uma imagem arquivada. Com o programa são fornecidas as imagens MAND1, MAND2, JULIA1 e JULIA2. Por baixo de cada conjunto de Julia, está indicado o valor de c correspondente. Se não existir uma imagem com o nome pretendido, o computador emite um pequeno sinal sonoro. A saída para o menu principal faz-se, tal como nos casos anteriores, clicando no quadrado do canto superior esquerdo.

O utilizador pode dar largas às suas possibilidades criativas: pode fazer, por exemplo, "zooms" sucessivos do conjunto de Mandelbrot ou produzir conjuntos de Julia para vários valores de c na fronteira do conjunto de Mandelbrot. Avisa-se, no entanto, que as imagens produzidas ocupam um espaço em disco que pode ser significativo.

4. CONTEÚDOS QUE ABRANGE E RELAÇÃO COM OS CURRÍCULOS ESCOLARES

Já alguém disse que o conjunto de Mandelbrot é a figura matemática mais complicada que existe. Mas não é apenas a sua forma extremamente recortada ("fractal") que é interessante: são-no também as suas propriedades matemáticas, que têm merecido a atenção de um grande número de investigadores. Os conjuntos de Mandelbrot e de Julia são exemplos de figuras de geometria fractal, uma forma de geometria criada pelo matemático francês Benoit Mandelbrot nos anos 70. O primeiro texto de apoio, de Jorge Silva e Carlos Fiolhais, procura introduzir a geometria fractal.

O tema dos fractais e o tema do caos que lhe está intimamente associado, por serem recentes, só agora estão a entrar nos currículos escolares tanto do ensino secundário como do ensino universitário. A experiência norte-americana de introdução dos fractais em escolas secundárias está apresentada nos dois volumes da obra "Fractals for the Classroom" (Springer, Nova Iorque, 1991), que é complementada por dois volumes de actividades, com numerosas fichas de trabalho e alguns diapositivos. Encontra-se aí um grande repositório de propostas para utilização pedagógica dos fractais, incluindo os conjuntos de Mandelbrot e de Julia.

Em Portugal, não foi utilizada a oportunidade recente da elaboração dos novos programas do ensino secundário para introduzir a geometria fractal. Acontece que os números complexos, necessários em príncipio para descrever os conjuntos de Mandelbrot e de Julia, não estão incluídos nos novos currículos. No entanto, já tem perfeito cabimento nos programas de matemática o estudo de processos iterativos usando números reais, sendo encorajado o uso da calculadora. Jaime C. Silva, no segundo texto de apoio do fim deste manual, explora essa via para ensaiar uma introdução às figuras fractais aqui discutidas. No livro de A. Dewdney, "A Máquina mágica" (publicado pela Gradiva em 1994, cujos três primeiros capítulos são transcritos no terceiro texto de apoio), também aparece uma abordagem do conjunto de Mandelbrot que evita o formalismo dos números complexos.

Os fractais aparecem hoje em vários sítios: em obras de arte, peças de design, livros de divulgação, filmes, programas de televisão, revistas e jornais, etc. Os computadores que os possibilitam chegaram primeiro à sociedade do que à escola, mas estão a alargar e consolidar o seu papel nesta última. Um dia, os fractais passarão das capas dos livros escolares, onde já hoje aparecem, para o seu interior...

5. Textos de Apoio

TEXTO 1 - O ESTRANHO MUNDO DOS FRACTAIS

1. INTRODUÇÃO

Bertrand Russel escreveu, em 1918, no seu livro "Misticismo e Lógica":

"A matemática possui não apenas a verdade, mas uma beleza suprema - uma beleza fria e austera como a de uma escultura".

Contudo, essa beleza apenas era perceptível para os matemáticos, habituados a lidar com os domínios abstractos da sua ciência. Recentemente, com o desenvolvimento de um novo ramo da geometria, a chamada "geometria fractal", uma parte daquela beleza tornou-se perceptível e evidente para mais gente. O surpreendente é que essa beleza ao nosso alcance se deve a uma evolução na forma de olhar a natureza.

Galileo Galilei afirmou, em 1626:

"O universo (...) não pode ser compreendido a menos que primeiro aprendamos a linguagem no qual ele está escrito. Ele está escrito na linguagem da matemática, e os seus caracteres são os triângulos, círculos e outras figuras geométricas, sem as quais é impossível compreender uma palavra que seja dele: sem estes ficamos às escuras num labirinto escuro."

Foram precisos cerca de 350 anos para surgir uma nova visão da natureza. Foi Benoit Mandelbrot, matemático francês contemporâneo, quem desenvolveu a noção de fractal. No seu livro "The Fractal Geometry of Nature", publicado em 1983, afirma :

"Porque é que a geometria é habitualmente descrita como fria e austera? Uma razão reside na sua inaptidão em descrever a forma de uma nuvem, de uma montanha, de uma linha costeira, de uma árvore. As nuvens não são esferas, as montanhas não são cones, as linhas costeiras não são círculos e a casca de uma árvore não é suave, nem os relâmpagos se propagam em linha recta(...) A natureza exibe não apenas um grau mais elevado, mas um nível de complexidade completamente diferente. O número de diferentes escalas de comprimento dos motivos naturais é para todos os efeitos infinito. A existência desses motivos desafia-nos a estudar aquelas formas que Euclides deixou de parte como não tendo uma forma definida, desafia-nos a investigar a morfologia do amorfo."

Nascia então a geometria fractal. Para podermos descrever o pormenor irregular e quase aleatório de muitos dos padrões da natureza, não nos podemos cingir à geometria tradicional. Com a geometria fractal, a matemática torna-se menos "fria" e "austera" e reconcilia-se, de certo modo, com a velha Natureza, que desde sempre lhe tem servido de motivo e inspiração.

2. O APARECIMENTO DA IDEIA DE FRACTAL

A evolução das ideias que deram origem aos fractais é curiosa. Diz Mandelbrot:

"Introduzi uma ideia que parecia síntese (...) mas que se iria revelar como a base da teoria dos fractais. A ideia era que, no estudo da variação dos preços, não havia nenhuma diferença de natureza entre as variações a curto e a longo prazo."

Com base nesta ideia, Mandelbrot desenvolveu um modelo matemático que lhe permitia fazer simulações da bolsa que os especialistas não distinguiam da situação real. Da especulação bolsista, passou ao estudo das turbulências atmosféricas e, mais tarde, à chamada "geografia quantitativa", um novo ramo da geografia. E, a partir da ideia de saber quanto media a costa da Grã-Bretanha, Mandelbrot adaptou e aplicou a sua teoria à síntese de imagens. Obteve imagens sobre as quais afirmou:

"As imagens que calculei com a minha teoria matemática assemelhavam-se curiosamente à realidade: e se eu podia imitar a natureza, era porque provavelmente teria descoberto um dos seus segredos..."

Um exemplo de fractais referido no livro de Mandelbrot é a fronteira entre dois países; aparece aí referenciada a fronteira entre Portugal e a Espanha a qual, poucos o sabem, é um fractal. Vejamos porquê.

Uma circunferência não é um fractal. O seu perímetro, definido pela fórmula 2pr, é finito. Para medir esse perímetro podemos colocar um polígono com um número cada vez maior de lados (triângulo, quadrado, pentágono, etc.) dentro da circunferência e calcular o perímetro do polígono. Obtemos, no limite em que o número de lados é infinito, um valor finito: precisamente 2pr.

Tentemos fazer algo de semelhante para a fronteira entre Portugal e Espanha. Comecemos por medir a fronteira utilizando sucessivamente réguas de 100 km, 10 km, 1 km, 1 m, etc.. O curioso é que o comprimento da fronteira vai aumentando progressivamente, à medida que se diminui a escala de observação (o processo experimental tem um limite, pois quando se chega aos átomos já não se sabe qual é o átomo espanhol e qual o átomo português...). Essas figuras cujo comprimento aumenta indefinidamente à medida que diminui a escala de medida são os fractais. Isto acontece porque existe um "rendilhado" em todas as escalas, quer em escalas pequenas quer em escalas grandes.

3. A AUTO-SEMELHANÇA E A DIMENSÃO FRACTAL

A auto-semelhança é uma ideia antiga. Contudo, e apesar de ser uma propriedade geométrica simples, apenas no início da década de 70 o homem se apercebeu da sua existência na Natureza. Se olharmos para o mundo à nossa volta, vemos uma infinita variedade de objectos com uma estrutura geométrica deveras complexa e intrincada: uma folha de feto, um cristal de neve, a superfície irregular de uma montanha, ou até mesmo uma descarga eléctrica num meio dieléctrico (de que o caso mais conhecido é o relâmpago). Se observarmos a estrutura microscópica destes objectos o que vemos? Algo bastante surpreendente: a parte é muito semelhante ao todo. Um fractal possui um número infinito de pequeninas cópias dele próprio: é a esta propriedade que se chama auto-semelhança.

A auto-semelhança está relacionada com o conceito de dimensão fraccionária, isto é, pode ser traduzida matematicamente por um coeficiente chamado dimensão fraccionária. Esta dimensão, diferente da dimensão topológica habitual (que é um número inteiro), serve para caracterizar o fractal. Os fractais são objectos matemáticos que se podem definir, segundo Mandelbrot, como "um conjunto (de pontos no espaço euclideano) para o qual a dimensão de Hausdorff excede a dimensão topológica".

Podemos obter a dimensão de um objecto usando o método que a seguir se descreve. Suponhamos que temos uma linha de comprimento L. Começamos por considerar uma linha de comprimento u e sobrepômo-la à linha L, e contamos quantas linhas u são necessárias para a cobrir completamente (fig 1). O número N=L/u representa uma medida da linha L. Analogamente, para medir um quadrado (cubo) de lado L, pegamos num quadrado (cubo) unitário de lado u e contamos o número N=L²/u² (N=L³/u³) de que necessitamos para cobrir o objecto. De uma maneira geral, este processo leva a N=(L/u)^d, ou, tomando o logaritmo de ambos os membros,

d = log N / log (L/u)    (1)

Para um objecto uniforme e compacto, d é um inteiro igual à dimensão topológica. Mas para um fractal tem-se que d é um número fraccionário: d é o que se chama dimensão de Hausdorff ou dimensão fractal.

Um dos exemplos mais simples é a chamada curva de Koch (fig. 2). Para formar a curva de Koch, começa-se por um segmento de recta e substitui-se pelo motivo ao centro de figura 2. Depois, substitui-se cada um dos segmentos resultantes pelo mesmo motivo, obtendo-se a curva do lado direito da figura, repetindo-se este processo "ad infinitum". A curva construída é um fractal, cuja dimensão é d_f = log 8 / log 4 = 1,5 (tem-se N=8 e o chamado factor de escala L/u é 4).

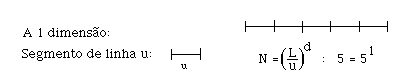
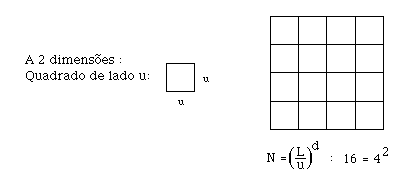
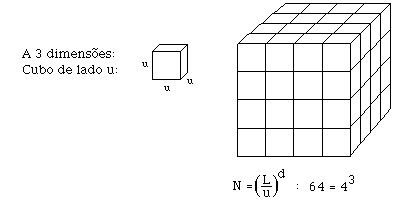
Figura 1

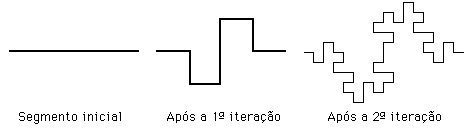
Figura 2

O "floco de neve" da fig. 3 foi obtido a partir da curva de Koch. Embora a sua área seja evidentemente finita, o seu perímetro é infinito.

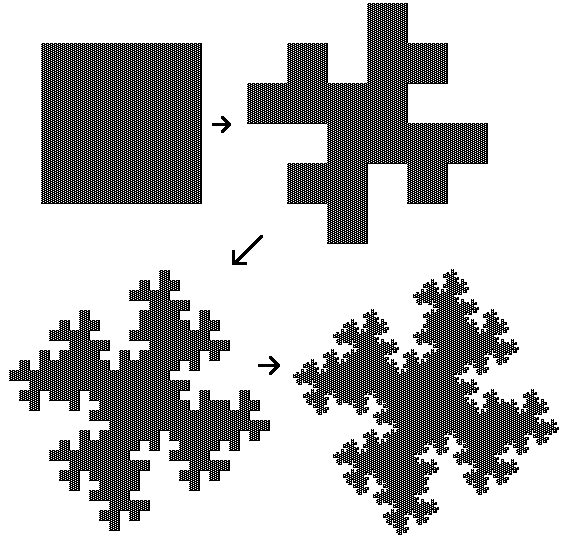
Figura 3

Um exemplo de um fractal no espaço a 3 dimensões é o seguinte. Começa-se por um cubo, formado de cubos mais pequenos (como o cubo de Rubik), e retiram-se os cubos do meio das faces e o cubo do centro. Repete-se o processo indefinidamente, obtendo-se um cubo completamente esburacado, com buracos de todos os tamanhos. Trata-se de um fractal de dimensão d_f=log 20 / log 3 = 2,727 (tiram-se 7 cubos aos 27 iniciais, e o factor de escala é 3). O cubo chama-se "esponja de Menger" e cada uma das suas faces é chamada "carpete de Sierpinski" (de dimensão d_f = log 8 / log 3= 1.893) Podiam dar-se muitos outros exemplos de fractais, todos eles estranhos e maravilhosos. Em cada um a propriedade de auto-semelhança confere-lhe o aspecto característico de fractal.

4. O CONJUNTO DE MANDELBROT

O estudo das fronteiras de estabilidade é um assunto extremamente actual. Um sistema particularmente simples mas suficientemente complexo é o conjunto de Mandelbrot. Ele é obtido submetendo os números do plano complexo (números da forma a+ib em que a e b são números reais e i é a constante imaginária) a um determinado processo. Como resultado da aplicação repetida deste processo, obtemos uma sequência de outros números complexos cuja norma (isto é, a distância à origem) pode ter um de dois comportamentos: ou se mantém finita e próxima de zero ou tende para infinito (basta para tanto ser maior que 2). É a fronteira entre estes dois domínios que delimita o conjunto de Mandelbrot. O processo iterativo que lhe dá origem baseia-se numa fórmula surpreendentemente simples:

z_n+1 = f(z_n) = z_n² + c (2)

em que tanto z como c são números complexos. Este processo iterativo é muito semelhante ao que aparece na fórmula de Feigenbaum de uma iteração unidimensional; a não linearidade indicada pelo quadrado é comum a ambos os casos.

Fazendo z₀= 0 e repetindo a iteração da fórmula (2) para vários valores da constante c, obtém-se o conjunto de Mandelbrot (figs 4 e 5). Dele fazem parte os pontos cuja norma não tende para infinito mesmo após um grande número de iterações. Os restantes números pertencem à região de instabilidade e permitem definir regiões de transição entre a estabilidade (que encontramos dentro do conjunto de Mandelbrot) e o caos, consoante a velocidade à qual a norma do número z tende para infinito. Esta transição é obtida através de uma regra geral, o que leva a concluir que até mesmo o caos tem as suas regras e o estudo de sistemas dinâmicos complexos e não-lineares está ao alcance de uma investigação e sistematização científicas.

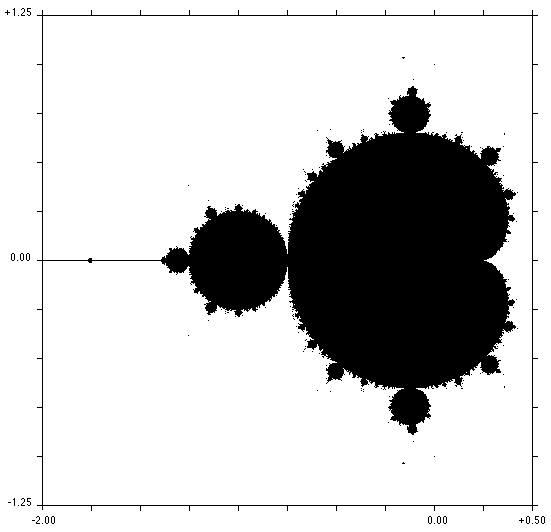
Figura 4 - O conjunto de Mandelbrot

A fronteira do conjunto de Mandelbrot é ela própria um fractal, já que é auto-semelhante. Vamos ver de seguida como é que o conjunto de Mandelbrot contém em si uma infinidade de fractais.

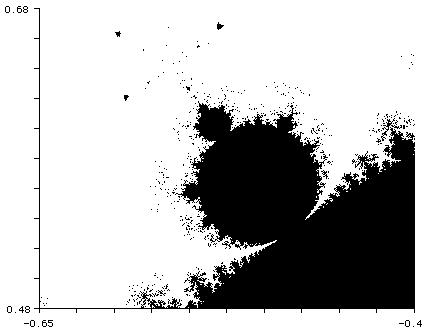
Figura 5 - Ampliação de uma região do conjunto de Mandelbrot

5. OS CONJUNTOS DE JULIA

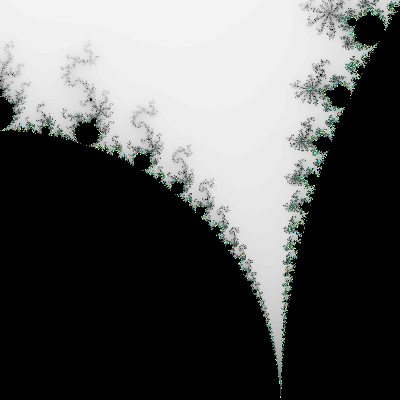
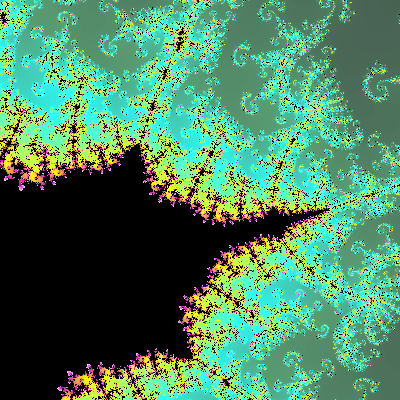
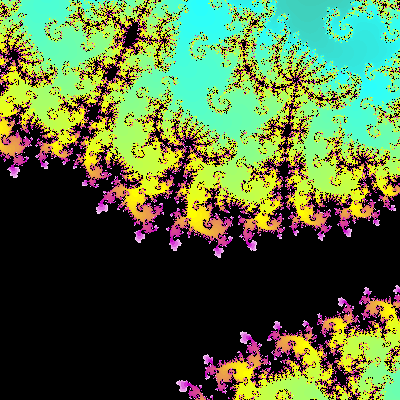
Para obter o conjunto de Mandelbrot aplicámos a fórmula (2) fazendo z₀= 0 e atribuindo a c valores do plano complexo. Se agora escolhermos para c um valor fixo (dentro do conjunto de Mandelbrot) e atribuirmos a zo valores do plano complexo, vamos obter, para cada valor de c figuras que são o conjunto dos valores de z que convergem no processo da iteração sucessiva definido por (2) (figs 6 a 8). Essas figuras são já conhecidas desde o início do século, tendo sido estudadas por Gaston Julia e Pierre Fatou, matemáticos franceses, mas só há pouco tempo, com a ajuda da computação gráfica, foi possível estudá-los em pormenor e compreender o seu significado e importância. Um dos aspectos curiosos é que a sua fronteira, chamada conjunto de Julia, é fractal, portanto auto-semelhante. Embora só haja um conjunto de Mandelbrot, existem infinitos conjuntos de Julia, um para cada ponto do conjunto de Mandelbrot, que funciona assim como "catálogo" de conjuntos de Julia. No conjunto de Mandelbrot existem "zonas geográficas" diferentes, que se identificam pela forma dos conjuntos de Julia respectivos (vale dos cavalos marinhos, região das dendrites, etc.). O ponto (0,0) é desinteressante: a figura associada é um círculo, que, como vimos, não é um fractal. As zonas mais interessantes são as que se situam nos bordos do conjunto de Mandelbrot. Saindo um pouco fora deste conjunto, as figuras de Julia desfazem-se em poeira, isto é, deixam de ser conexas.

Figura 6 - Conjunto de Julia para c = -0.39054 -0.58679i

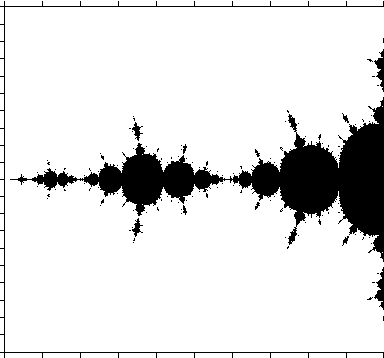
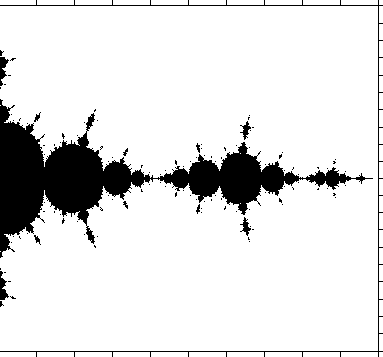
Figura 7 - Conjunto de Julia para c = -1.25 + 0.0i

Uma noção relevante que aparece na análise destes conjuntos é a de atractor. No caso presente, um atractor é um ponto ou um conjunto de pontos para os quais a iteração de outros pontos do plano complexo converge. Os conjuntos de Julia delimitam bacias de atracção. A noção de atractor já é conhecida desde Henri Poincaré, tendo sido aplicada a sistemas dinâmicos dissipativos: verifica-se que a sua evolução temporal é condicionada pela existência de um atractor. Na mecânica clássica estudam-se normalmente sistemas cujos atractores são pontos, círculos ou outras figuras simples. Contudo, estes casos são excepções e o comportamento de muitos sistemas (os sistemas dinâmicos não-lineares) é bem mais complicado: os seus atractores e repulsores (estes, como o nome indica, são regiões de equilíbrio instável) podem ser fractais. Em particular, os chamados "atractores estranhos" mais não são do que exemplos de fractais (por exemplo a figura de Lorentz, que aparece no estudo computacional dum fluido viscoso).

Figura 8 - Conjunto de Julia para c = 0,27334 + 0,00742i

6. UM FRACTAL DE INTERESSE FÍSICO

Na natureza são inúmeros os objectos que crescem por adição aleatória de novos constituintes. Exemplos disso são as dendrites que crescem na água quando esta é arrefecida abaixo do ponto de congelação. Em muitos casos, o crescimento do objecto é condicionado pela difusão das novas partículas até à superfície do agregado já existente. Um modelo simples surgido recentemente (em 1981) e que simula este fenómeno de crescimento de agregados é a chamada "Agregação Limitada por Difusão" ("Diffusion Limited Aggregation", DLA). As regras deste modelo são simples e o algoritmo que as realiza num computador é também simples. Começa-se por colocar uma semente no ponto central de uma rede. De seguida larga-se uma segunda partícula dum ponto aleatório sobre uma circunferência suficientemente distante da semente. Simula-se então a difusão dessa partícula através de um passeio aleatório, isto é, a partícula move-se aleatoriamente pela rede até chegar a um dos pontos adjacentes ao ponto inicialmente ocupado. Nessa altura ela é capturada, passando a integrar o agregado. Uma nova partícula é então lançada de local e em direcções aleatórias até ser capturada, repetindo-se o ciclo. Formam-se assim agregados (fig. 9) em tudo semelhantes às dendrites, ou à descarga eléctrica num meio dieléctrico.

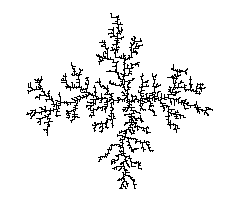
Figura 9 - Agregado gerado por DLA com 3486 pontos

Um fenómeno curioso e que, no fundo, está por detrás do aspecto ramificado dos agregados produzidos pela DLA é o efeito de protecção que os pontos mais exteriores do agregado exercem sobre os mais interiores. Isto deve-se ao facto de os caminhantes aleatórios não conseguirem penetrar no agregado para ocupar os pontos mais centrais ainda livres, uma vez que são capturados pelos pontos mais exteriores. Existem assim reentrâncias de todos os tamanhos.

É possível determinar a dimensão de uma figura de DLA, chegando-se à conclusão que se trata de uma dimensão fraccionária (d_f = 1,67 para uma rede quadrangular a 2 dimensões). O modelo da DLA conduz portanto a fractais, embora estes fractais sejam estatísticos, pois a sua regra de construção não é perfeitamente determinista.

7. CONCLUSÃO

"A Arte é uma mentira que nos permite reconhecer a verdade"

Pablo Picasso

As figuras fractais geradas pelos métodos descritos (e muitos outros existem!) podem ser classificadas de extremamente belas, embora isso seja uma opção estética e portanto pessoal. Contudo, não é o facto de haver arte nos desenhos dos fractais que é importante (assunto relativamente ao qual a opinião de artistas e cientistas pode ser diferente), mas sim o facto de os fractais mostrarem que também os sistemas complexos são passíveis de um estudo sistemático, que até o caos tem as suas regras. Os matemáticos e os físicos já não estão limitados ao estudo de sistemas simples e lineares: têm diante de si o mundo real, bem mais complexo e fascinante.

Jorge Alexandre Silva

Carlos Fiolhais

As figuras foram obtidas pelo primeiro autor usando um programa em linguagem Pascal para um computador Macintosh.

TEXTO 2 A MATEMÁTICA E O CAOS- I E II

I - A matemática e o caos

O caos está na moda. Fala-se de caos na política e na economia quase todos os dias. A palavra "caos" tem uma conotação tão forte que foi aproveitada pelos cientistas, em particular por físicos e matemáticos; como é óbvio, a imprensa fala do caos no sentido corrente e não do caos no sentido científico. A teoria de caos é uma matéria científica de desenvolvimento recente.

Vejamos alguns exemplos de utilização da palavra "caos" pela imprensa:

Pelo contrário, figuras como as abaixo, muito populares, referem-se ao caos matemático (a primeira é o conjunto de Mandelbrot e a segunda um conjunto de Julia).

Mas o que é o caos na Matemática?

Vamos começar por fazer duas experiências com a calculadora (elas podem também ser feitas com um computador, com o mesmo resultado).

Experiência 1

Seja f(x) = x² - 2 e x₀ Î R. Definamos a sucessão (x_n) por indução por meio de

x_n = f(x_n-1), n Î N.

Vamos determinar os primeiros termos de algumas destas sucessões para diversos valores de x₀.

Usando uma calculadora completa a tabela abaixo:

Regista apenas as primeiras três casas decimais (sem arredondar).

(Usando a calculadora TI-68 basta escrever uma fórmula como X = X x X - 2 e ir sucessivamente calculando essa fórmula para cada novo valor de X; não convém limitar o número de casas decimais por causa dos arredondamentos inconvenientes; para anular a limitação de casas decimais carregar em [2nd][Fix][.]).

Repara que não é por x₀ se aproximar de zero que os termos da sucessão se vão aproximando dos termos da sucessão gerada por x₀=0.

Mas o mais curioso é que a tabela preenchida depende da calculadora (ou do computador) usada.

Sim, depende! Se um teu colega usou uma calculadora diferente compara os teus resultados com os dele. O autor de um texto sobre o assunto (Robert L. Devaney) obteve a tabela seguinte:

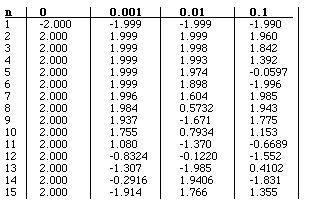
Observa como os valores variam de máquina para máquina! (Observa contudo que algumas diferenças são apenas devidas a diferenças no modo como a máquina arredonda o resultado.)

Experiência 2

Seja g(x) = 100x (mod 1), isto é, g(x) é a parte fraccionária de 100x. Seja x₀ Î [0,1]. Definamos a sucessão (x_n) por indução por meio de

x_n =g(x_n-1), n Î N.

a) Escolhe primeiro x₀=3/2 . Determina os vinte primeiros termos da sucessão, primeiro à mão e depois usando a calculadora.

b) Escolhe agora x₀= p/4. Determina os vinte primeiros termos da sucessão, usando a calculadora.

c) Escolhe um qualquer x₀ Î [0,1]. Determina os vinte primeiros termos da sucessão, usando a calculadora. (Na calculadora TI-68 basta escrever uma fórmula como X = frc(100 x X) e ir sucessivamente calculando essa fórmula para cada novo valor de X; não convém limitar o número de casas decimais por causa dos arredondamentos inconvenientes).

O que aconteceu nos dois casos não foi bem o "caos" mas apenas aquilo que se designa por dependência sensível das condições iniciais, ou seja, uma variação das condições iniciais, neste caso o x₀, ainda que pequena, provoca grandes variações nos termos subsequentes. Foi o que aconteceu no primeiro quadro que construíste quando, tomando x₀ próximo de zero, o comportamento da sucessão veio totalmente diferente do da sucessão gerada por x₀=0.

Outra manifestação do mesmo fenómeno nesta mesma experiência reside no facto de diferentes máquinas (mas não demasiado diferentes, não usámos nenhum computador de grande porte - uma estação de trabalho ou um supercomputador!) produzirem resultados diferentes pois trabalham internamente com um número diferente de casas decimais, e havendo dependência sensível das condições iniciais, uma alteração, nem que seja na 14º casa decimal, pode influir de modo decisivo no resultado.

A segunda experiência é ainda uma manifestação clara do mesmo fenómeno, pois qualquer que seja o arredondamento efectuado, este vai influir de forma tão decisiva no resultado final que a sucessão se anula sempre, a partir de certa ordem!

Para definir CAOS necessitamos de noções de topologia (ver a segunda parte desta actividade).

Para já podemos apenas definir um sistema dinâmico com dependência sensível das condições iniciais. Um sistema dinâmico é uma sucessão obtida por iteração de uma função, como fizemos nas duas experiências.

Definição: Diz-se que um sistema dinâmico possui dependência sensível das condições iniciais se e só se existe algum d positivo tal que para todo o x₀ Î [0,1] e para todo o e positivo, podemos encontrar um Y₀ Î [0,1] tal que, para todo o m Î N, temos

     |x₀ - y₀| < e

e

     |x_m - y_m| > d ,