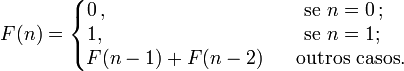Leonardo Fibonacci
Leonardo Fibonacci, também conhecido como Leonardo de Pisa, Leonardo Pisano ou ainda Leonardo Bigollo, (Pisa, c. 1170 — Pisa ?, c. 1250) mas, na maioria das vezes, simplesmente como Fibonacci foi um matemático italiano, tido como o primeiro grande matemático europeu do Medievo. É considerado por alguns como o mais talentoso matemático ocidental da Idade Média. Ficou conhecido pela descoberta da sequência de Fibonacci e pelo seu papel na introdução dos algarismos arábicos na Europa.
Com outros matemáticos do seu tempo, contribuiu para o renascimento das ciências exatas, após a decadência do último período da antiguidade clássica e do início da Idade Média, mas Fibonacci destacou-se ao escrever o Liber Abaci, em 1202 (atualizado em 1254), a primeira obra importante sobre matemática desde Eratóstenes, isto é, mais de mil anos antes. O Liber Abaci introduziu os numerais hindu-arábicos na Europa, além de discutir muitos problemas matemáticos.
Fibonacci é também conhecido pela sequência
numérica nomeada após sua morte como sequência de
Fibonacci. Ele não descobriu, mas usou-a como
exemplo no Liber Abaci.
A Sequência de Fibonacci:
A Sequência de Fibonacci consiste em uma sucessão de números, tais que, definindo os dois primeiros números da sequência como 0 e 1, os números seguintes serão obtidos por meio da soma dos seus dois antecessores. Portanto, os números são: 0,1,1,2,3,5,8,13,21,34,55,89,144,233,...
Dessa sequência, extrai-se o número transcendental conhecido como número de ouro.
A sequência de Fibonacci é dada pela fórmula:
Retirado de
http://pt.wikipedia.org/wiki/Leonardo_Fibonacci
Aplicações
na natureza:
Couve-flor comum:

Aqui está uma foto de uma couve-flor comum. Note como ele é quase um pentágono em linhas gerais. Olhando com cuidado, você pode ver um ponto central, onde as florzinhas são menores. Olha novamente, e você vai ver as florzinhas são organizadas em espirais em torno deste centro em ambas as direções.
Quantas espirais há em cada sentido?


Broccoli
romântica / Couve-flor (ou Romanesco):

Broccoli românica / Couve-flor (ou Romanesco) parece e tem gosto de um cruzamento entre brócolis e couve-flor. Cada flósculo é pico e é uma versão idêntica, porém menor da coisa toda e isso faz com que as espirais fácil de ver.
Quantas espirais há em cada sentido?
As imagens em baixo mostra as espirais de forma mais
clara para você contar (as linhas são
desenhadas entre os floretes):


Um Filme de Aplicações da Sequência de Fibonacci:
Outras sucessões do tipo da de Fibonacci:
| 1 |
1 |
1 |
1 |
4 |
7 |
13 |
25 |
44 |
... |
| 1 |
2 |
3 |
5 |
8 |
13 |
21 |
34 |
55 |
... |
| 1 |
2 |
3 |
6 |
11 |
20 |
37 |
68 |
125 |
... |
| 1 |
3 |
5 |
9 |
17 |
31 |
57 |
105 |
193 |
... |
É
Fim
Deste
Relato
Faça Agora
Um Fib belo e pessoal
Será este o primeiro internacional?
Retirado de http://www.digestivocultural.com/blog/post.asp?codigo=850&titulo=Poesia_em_Fibonacci em 27 de Março de 2012
| “ |
One |
” |
|
—Pincus, Gregory K.[1] |
||
"Um
Pequeno,
Preciso,
Poético,
Mistura em espiral:
Matemática mais poesia produz o Fib."
Retirado de http://en.wikipedia.org/wiki/Fib_%28poetry%29 em 27 de Março de 2012