Home Page

A PROPÓSITO DE UM PROGRAMA DE COMPUTADOR:
DINÂMICA DE CORDAS VIBRANTES
Hugo R.P. Caldeira*

Não pretendo estender-me demasiado acerca do tema (que poderá ser encontrado com maior rigor de análise em tratados de Mecânica Geral); escrevo aqui apenas em traços largos o que se poderá chamar de pretenso convite para uma posterior análise do tema a quem lhe aprouver, talvez depois de visionar o programa que serviu de motivação para este trabalho, ou outro programa semelhante,

Parafraseando o Prof. Artur Alves** "A mecânica ocupa-se da forma mais elementar do movimento a simples mudança de lugar". Daqui o interesse do estudo da dinâmica de cordas vibrantes, onde se pretende obter uma função que traduza a posição ocupada pela corda em cada instante t. Quotidianamente, quando se fala sobre cordas vibrantes, formulamos quase inconscientemente uma serie de condições relacionadas com o facto de estarmos a falar de uma corda e, particularmente, de uma corda que vibra: supomos que ela está necessariamente fixa em dois pontos, sugerindo que se trata de uma corda finita que vibra entre esses dois pontos.

Na Mecânica dos meios contínuos, para o estudo da corda vibrante, necessitamos de um modelo matemático que permita simular o comportamento de uma corda vibrante, Como todos os modelos, este seria uma aproximação à realidade da corda vibrante; daí que, para obtermos uma dinâmica no nosso modelo o mais fiel possível à realidade, temos de lhe impor determinadas condições, chamadas as hipóteses das pequenas oscilações. São elas:

i) a corda tem um comprimento fixo L;

ii) a tensão é constante ao longo da corda e do tempo;

iii) a densidade da corda é constante ao longo da corda e do tempo;

iv) os pontos da corda movimentam-se num plano (onde vou considerar um referencial ortonormado);

v) a corda só está sujeita à força de reacção nos seus extremos;

vi) a velocidade de cada ponto é perpendicular a recta que passa pelos seus pontos extremos (eixo das abcissas),

Repare-se que a "nossa corda" é agora considerada um corpo inextensível e contínuo: daí que determinados comportamentos observáveis numa corda real, o não sejam neste modelo, nomeadamente o facto do período de tempo ao longo do qual uma corda real vibra ser directamente proporcional à intensidade das forças exteriores que sobre ela actuam e isto devido à corda ser extensível e à sua tendência natural para regressar à posição de repouso - veja-se o caso das cordas de uma viola acústica

A partir da equação diferencial da corda vibrante,

(onde u(x,t) nos diz a posição do ponto da corda cuja abcissa é x no instante t, sendo c a velocidade das ondas), considerando t=0 para instante inicial e dadas as posições iniciais u(x,0)=u0(x) e as velocidades iniciais

pretende-se determinar uma função u(x,t), para 0 <x< L e 0< t< +, onde as condições u(0,t)=0 e u(L,t)=0 têm de ser satisfeitas para garantir a imobilidade dos pontos extremantes da nossa corda. Estamos assim num caso particular do Problema de Cauchy,

Algumas paginas mais tarde através de uma conveniente mudança de variável, concluímos

a função representativa do movimento da corda vibrante, Repare-se que sendo poderemos arranjar cordas de comportamento idenitico para uma adequada escolha da massa e da tensão a que estão sujeitos nomeadamente, podemos obter c=1. pelo que se justifica a redução do estudo da corda vibrante (finita ou não) ao estudo da porção de corda cujos extremos são x=0 e x=L, fixos ao longo do tempo.

Na monografía que elaborei acerca deste tema., tive oportunidade de apresentar um programa (em linguagem LOGO), que permite a visualização da configuração de cordas vibrantes (pré-definidas. com e sem velocidade inicial), em momentos t igualmente espaçados. Refira-se aqui que, dada a simplicidade facilmente se prova que esta função e periódica em x (período 2L) e ímpar, permitindo~nos concluir que o gráfico de uma corda vibrante infinita é do tipo

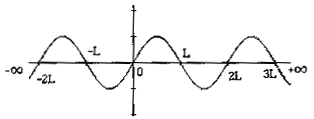
do programa, este e facilmente adaptado a qualquer outra linguagem.

Para terminar, gostaria de salientar o caso particular da corda