Fibonacci.mws

Sucessão de Fibonacci

Resolução da relação de recorrência que a define

17/10/2007

Procedimento que calcula, por recursão, o n-ésimo termo da sucessão de Fibonacci

>    Fibonacci := proc(n::posint) option remember;

>       if n=1 or n=2 then RETURN( 1 ); fi;

>       Fibonacci(n-1) + Fibonacci(n-2);

>    end:

>    seq(Fibonacci(i), i=1..20);

1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765

Cálculo das raízes da equação característica

>    evals := solve(x^2-x-1,x);

evals := 1/2+1/2*5^(1/2), 1/2-1/2*5^(1/2)

Resolução do sistema com as condições iniciais

>    sol := solve({

>        c1 * evals[1] + c2 * evals[2] = 1,

>        c1 * evals[1]^2 + c2 * evals[2]^2 = 1

>        },

>        {c1,c2});

sol := {c2 = -1/5*5^(1/2), c1 = 1/5*5^(1/2)}

Fórmula fechada do n-ésimo termo de Fibonacci

>    Fn := c1 * evals[1]^n + c2 * evals[2]^n;

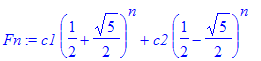
Fn := c1*(1/2+1/2*5^(1/2))^n+c2*(1/2-1/2*5^(1/2))^n

>    c1 := sqrt(5)/5; c2 := -sqrt(5)/5;

c1 := 1/5*5^(1/2)

c2 := -1/5*5^(1/2)

Cálculo dos primeiros 20 números de Fibonacci pela fórmula fechada.

>    simplify(c1 * evals[1]^10 + c2 * evals[2]^10);

55

>    seq(simplify(c1 * evals[1]^i + c2 * evals[2]^i), i=1..20);

1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765

>    solve(x^2-2*x-2,x);

1+3^(1/2), 1-3^(1/2)

>