Usually, the coordinates of a point over the earth's surface are described for the Geographic Longitude (l) and Latitude (j), these values are indeed linked to the Equatorial Coordinates that are more used in Astronomy. However, these two systems of coordinates are oriented parallel to the equator plane and to the Earth's rotational axis.

    The conversion between Declination (d) and the Geographic Latitude will be immediately if the Earth was a perfect sphere, since that in this case the both were equal, however, since that the Earth have the form of a Flattening Revolution Ellipsoid, the concept of Geographical Latitude must be careful study.

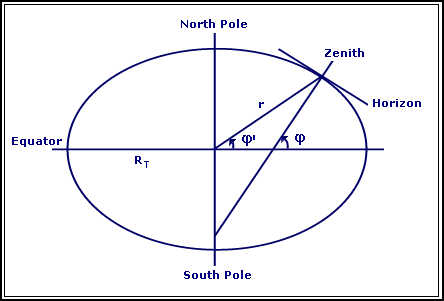
    The latitude represents the angle between the local horizon at any point and the Earth axis as the following picture describes:

Fig. 01: Flattening of the Earth

    Taking a transverse slice passing through the North and South poles, we can observe that the resulting section it's an ellipse to the one witch the horizon is tangent. So, we may conclude that the Latitude it's not the equal to the Geocentric Latitude (j'). Both these values describes the angle between the position vector and the equatorial plane. By the next equations, we can see the relationship between the latitude and the geocentric latitude:

r·cos(j') = R_E´(1 - e²sin²j)^-½´cosj

r·sin(j') = (1 - e²)´R_E´(1 - e²sin²j)^-½´cosj

tan(j') = (1 - e²)´tanj

where:    R_E: Earth's Equatorial Radius;

             e: Eccentricity of the Earth's Ellipsoid.

    Due to the Centrifugal Force produced by the rotation of the Earth, she deforms so that the equatorial radius it's about 20Km bigger that the distance between the poles. The relationship between these two values defines the flattening. So we have:

f = (R_E - R_POLES)/R_E = 21.385/6378.14 = 0.003353

    So, we can concluded that the eccentricity is:

e = (1 - (1 - f)²)^½ = (2f -f²)^½

    For these calculations it's not necessary to define the geographic latitude by the correct formulas, so we are going to use the following approximation:

j = j' + 0º.1924sin(2j')

    Only the geographic longitude it's missing. This one are almost equal to the right ascension, the only difference is that the right ascension is measuring through the Vernal Point and the geographic longitude it's referred to a fixed point of the Earth.

    These coordinates will differ essentially by one angle Q₀(t), that is dependent of the Earth rotational movement at each instant t (see Time and Calendars section: Sidereal Time).

Solar Eclipses - Introduction;

Geometry of the Solar Eclipses;

Duration of a Solar Eclipse.