Eclipses - Solar Eclipses: Geometry
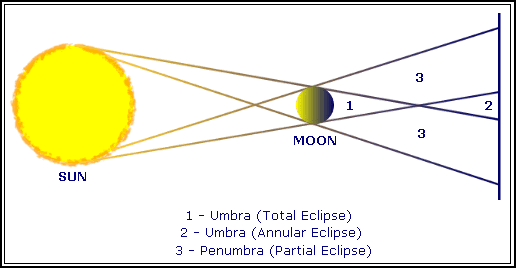
The light rays emitted by the Sun produces two shadow zones with the form of cones, at we call Umbra and Penumbra.
There are three types of Solar Eclipses: Totals, Annular and Partials. In the following figure are represented the umbra and the penumbra as also the zones where occurs the different types of solar eclipses.

Fig. 01: Umbra and Penumbra
The distance between the Earth and the Moon it's approximately 380 000Km, but due to the eccentricity of the Moon's orbit, this value can vary more or less 25 000Km. In the spite of this, during an Eclipse, the Earth are always very close to the point of the Umbral cone. Even at the Perigee, the umbral shadow's diameter in the Earth's surface it's rarely bigger than 200Km. At the Apogee, the Eclipse is Annular.
If we measure in a perpendicular plane the straight line that unifies the Sun with the Moon, and at a distance S behind the Moon, the Umbral diameter (d) and the Penumbral one (D) will be:
d(S) = DS(S/rSM) - DM(1 + S/rSM)
D(S) = DS(S/rSM) + DM(1 + S/rSM)
where: DS: Sun's diameter;
DM: Moon's Diameter;
rSM: Distance between the Sun and the Moon.
Now, it will be necessary to determinate the shadow's diameter at a distance (s) from the Moon. For that consider the following scheme:
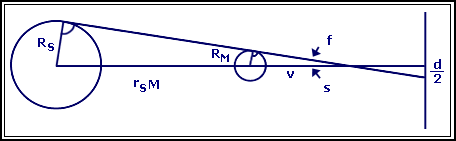
Fig. 02: Shadow Diameter Calculation
From the scheme we take:
| v´sin(f)=RM | e | sin(f)´(v + rSM) = RS |
| sin(f) = (RS - RM)/rSM | e | v = RS´rSM/(RS - RM) |
Therefore the shadow's diameter ‘d’ at the distance ‘s’ from the Moon will be:
d = 2(s - v)´tan(f)
» 2(s - v)´sin(f)
= 2 RS(s/rSM) - 2RM(1 + s/rSM)
The Umbra's position on the Earth can be obtain by the intersection of a straight line that pass by the centre of the Moon and by the centre of the Sun. To describe the direction of that straight line we may consider the unitary vector e, that can be calculated through the coordinates of the Sun and Moon's position vectors.
Schematic, we have:
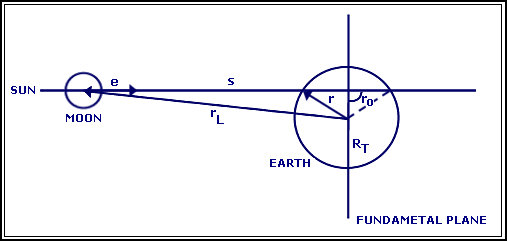
Fig. 03: Intersection of the shadow's axis with the Earth
Now it's possible to determinate any point r of the shadow using the vector e:
r = rM + s´e with e = (rM - rS)/|rM - rS|
If we consider the Earth as being a perfect sphere with radius RE, the distance s between the desired point and the centre of the Moon, and transforming to the vector coordinates, will be:
[x y z]T = [xM yM zM]T + s[eX eY eZ]T
where:
r2 = x2 + y2 + z2 = RE2
Mixing both expressions with have an equation of the second degree:
s2 + 2(rM·e)s + (rM2 - RE2) = 0
That the solutions are:
| s = |
s0 -
|
|
s0 +
|
where: s0 = -rM·e = -(xMeX + yMeY +zMeZ)
D = s02 + RE2 - rM2
The value s0 represents
the Moon's distance to the Fundamental Plane (perpendicular plane to the
central axis of the shadow that pass on the centre of the Earth). The desired
intersection point will dist
![]() from
the fundamental plane for the side where the Sun and Moon are in that moment
(the second intersection point it will be on the fraction of the Earth that is
night in that moment, so we can eliminate it). Mixing the equations we can
obtain the Umbra's coordinates on the Earth's surface:
from
the fundamental plane for the side where the Sun and Moon are in that moment
(the second intersection point it will be on the fraction of the Earth that is
night in that moment, so we can eliminate it). Mixing the equations we can
obtain the Umbra's coordinates on the Earth's surface:
r = rM + (s0 -
![]() )·e
)·e
However, a Solar Eclipse starts before his Central Phase, in other words at the moment that the Penumbral shadow touches the Earth, a Partial Eclipse occurs somewhere. So it is important to distinguish the different phases of the Eclipse. For that, and considering the Umbra the Penumbra's diameters on the Fundamental Plane d0 and D0 respectively and r0 = (rM2 - r02)½, we have:
| RE + D0/2 | < | r0 | ® | No Eclipse | ||
| RE + |d0|/2 | < | r0 | < | RE + D0/2 | ® | Partial Phase |
| RE | < | r0 | < | RE + |d0|/2 | ® | Non Central Phase |
| r0 | < | RE | ® | Central Phase |
![]()
In this study in have assumed that the Earth was an perfect sphere, but it isn't true. So to calculate the true Solar Eclipses we need to made same corrections.
The Earth can be consider as an Sphere that suffer a flattening of:
1 - f = 0.996647
In other words, in a good geometric approach to the Earth aspect it's the ellipsoid. So, any point over the ellipsoid it will be the following equatorial coordinates:
r2 = x2 + y2 + z2/(1 - f)2 = RE2
The advantage to represent the Earth in this way it's the easy determination of the Umbra's shadow.
The 'z' coordinates of the Sun and the Moon are multiplied by 1/(1-f), and next we unified with a straight line these new positions and determinate the new intersection point wit the sphere of radius RE. The only difference between this point and the real point it's the 'z' coordinate that is bigger due to the factor 1/(1-f).
Using this procedure the all study are valid, so there's no need to make any adjustments.
Solar Eclipses - Introduction;