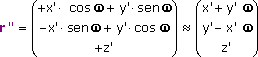
Eclipses - Solar Eclipses: Duration
The duration of the Total or Annular phase of an Eclipse it's not the same for all the points in the central line. If we ignore the diameter of the Umbra this difference (t + Dt) will depend almost of the velocity of the shadow moving among the Earth's surface.
An exact process for the calculation of the total duration requests many iteratively and will have an enormous computational weight, so we are going to use a lighter but also effective process. Consider the points that the shadow's axis cross the Earth:
r = (x,y,z)
r' = (x',y',z')
The difference between these two vectors will be one measure for the velocity of the umbral shadow. However this difference don't gives us the shadow movement due to the Earth's surface.
We can now define an angle w, as the angle that the Earth rotate in a Dt period:
w = 2p·Dt/1426 (radians)
For a point in the Earth's surface that haves r'=(x',y',z') as equatorial coordinates at the time (t + Dt), his coordinates at the time t will be:
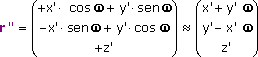
The way that the umbra's centre walk through the Earth's surface during a time interval Dt is:
| Dr = r'' - r | or |
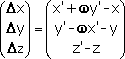 |
If e=(eX, eY, eZ) describes the direction of the shadow's axis, then Dr can be written as two components, one (Dr||) parallel to e and another (Dr^) perpendicular to the shadow's axis. So, we have:
Dr|| = Dr·e = DxeX + DyeY + DzeZ
Dr^ = (Dr2 - Dr||2)½
Now we can, finally, calculate the duration (t) of the Eclipse from the Total or Annular Phase for a diameter |d| of the Umbral Cone:
t = |d|/Dr^·Dt
Solar Eclipses - Introduction;