Eclipses - Eclipses Solares: Geometria
Os raios de luz emitidos pelo Sol produzem duas zonas de sombra em forma de Cones, às quais se dá o nome de Umbra e Penumbra.
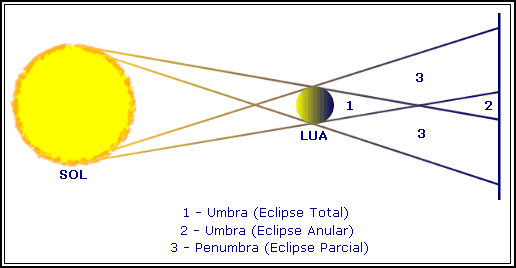
Existem três tipos distintos de Eclipses Solares: Totais, Anulares e Parciais. Na figura seguinte estão representadas tanto a Umbra como a Penumbra e os locais onde ocorrem os diferentes tipos de Eclipses Solares.
Fig. 01: Umbra e Penumbra
A distância da Terra à Lua é aproximadamente 380 000Km, mas devido à excentricidade da órbita da Lua este valor pode sofrer variações da ordem dos 25 000Km. Apesar disto, durante um Eclipse, a Terra encontra-se sempre muito próxima do ponto do cone da Umbra. Mesmo no Perigeu o diâmetro da sombra umbral na superfície da Terra é raramente superior a 200Km. No Apogeu o Eclipse é anular.
Se medirmos num plano perpendicular a recta que une o Sol e a Lua, e a uma distância S por detrás da Lua, os diâmetros da Umbra (d) e da Penumbra (D) ficam:
d(S) = DS(S/rSL) - DL(1 + S/rSL)
D(S) = DS(S/rSL) + DL(1 + S/rSL)
sendo: DS: Diâmetro do Sol;
DL: Diâmetro da Lua;
rSL: Distância entre o Sol e a Lua.
Torna-se agora necessário determinar diâmetro da sombra a uma certa distância (s) da Lua. Para tal considere-se o seguinte esquema:
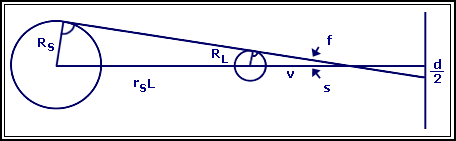
Fig. 02: Cálculo do diâmetro da Sombra
Do esquema tira-se que:
| v´sin(f)=RL | e | sin(f)´(v + rSL) = RS |
| sin(f) = (RS - RL)/rSL | e | v = RS´rSL/(RS - RL) |
Logo o diâmetro ‘d’ da sombra à distância ‘s’ da Lua fica:
d = 2(s - v)´tan(f)
» 2(s - v)´sin(f)
= 2 RS(s/rSL) - 2RL(1 + s/rSL)
A posição da Umbra na Terra pode ser obtida pela intersecção de uma recta que passa pelo centro da Lua e pelo centro do Sol. Para descrever a direcção desta recta considera-se o vector e, unitário, e que pode ser calculado através das coordenadas dos vectores posição da Lua e do Sol.
Esquematicamente tem-se:
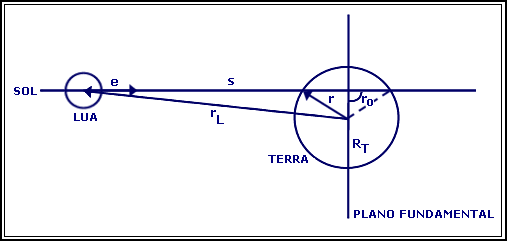
Fig. 03: Intersecção dos eixos da Sombra com a Terra
É possível determinar qualquer ponto r da sombra a partir do vector e, fazendo:
r = rL + s´e com e = (rL - rS)/|rL - rS|
Se se considerar a Terra como sendo uma esfera de raio RT, s a distância entre o ponto pretendido e o centro da Lua, e passando para os componentes de cada vector tem-se:
[x y z]T = [xL yL zL]T + s[eX eY eZ]T
donde:
r2 = x2 + y2 + z2 = RT2
Conjugando as duas equações fica-se com o seguinte equação quadrática:
s2 + 2(rL·e)s + (rL2 - RT2) = 0
Que admite como soluções os seguintes valores:
| s = |
s0 -
® Parte de Dia na Terra |
|
s0 +
® Parte de Noite na Terra |
onde: s0 = -rL·e = -(xLeX + yLeY +zLeZ)
D = s02 + RT2 - rL2
O valor s0 representa
a distância da Lua ao Plano Fundamental (plano perpendicular ao eixo central da
sombra e que passa no centro da Terra). O ponto de intersecção pretendido vai
ser o ponto que dista
do
Plano Fundamental para o lado onde se encontra o Sol e a Lua (o segundo ponto de
intersecção, visto situar-se na parte da Terra que está de noite, não vai ser
relevante neste estudo). Combinando as equações determinam-se as coordenadas da
Umbra na superfície da Terra:
r = rL + (s0 -
)·e
Contudo um Eclipse Solar começa antes da sua Fase Central, isto é, mal a sombra penumbral toca na Terra um Eclipse Parcial é observado algures. É importante, portanto, distinguir as diferentes fases do Eclipse. Para tal considerando-se os diâmetros da Umbra e da Penumbra no Plano Fundamental, d0 e D0 respectivamente e r0 = (rL2 - r02)½, tem-se:
| RT + D0/2 | < | r0 | ® | Ausência de Eclipse | ||
| RT + |d0|/2 | < | r0 | < | RT + D0/2 | ® | Fase Parcial |
| RT | < | r0 | < | RT + |d0|/2 | ® | Fase Não Central |
| r0 | < | RT | ® | Fase Central |
Neste estudo assumiu-se que a Terra é esférica, mas tal não acontece. Para se proceder ao cálculo dos Eclipses considerando uma melhor aproximação da superfície da Terra é necessário efectuar algumas correcções.
A Terra pode ser considerada como uma esfera de raio RT que sofreu um achatamento da ordem:
1 - f = 0.996647
Ou seja, uma boa aproximação geométrica para a forma da Terra é o Elipsóide. Assim sendo, qualquer ponto figura geométrica terá as seguintes Coordenadas Equatoriais:
r2 = x2 + y2 + z2/(1 - f)2 = RT2
A vantagem de representar a Terra desta maneira é a fácil determinação da posição correcta da sombra umbral.
As coordenadas 'z' do Sol e da Lua são multiplicadas pelo factor 1/(1-f). De seguida une-se com uma recta estas novas posições e determina-se o ponto de intersecção desta com a esfera de raio RT. A única diferença entre este ponto e o verdadeiro ponto de intersecção é que a coordenada 'z' é maior devido ao factor 1/(1-f).
Usando este procedimento, o estudo anterior é válido, não sendo preciso efectuar alterações.
Eclipses Solares - Introdução;