História da cultura das
Matemáticas em Portugal no século XVI
Estado de Portugal no século XVI
Álvaro Tomaz e Gaspar Nicolas,
aritméticos
Pedro Nunes como cosmógrafo
Pedro Nunes na Física
A Cosmologia na obra de Pedro
Nunes
Pedro Nunes na Geometria
Pedro Nunes na Álgebra
Considerações gerais sobre os
trabalhos de Pedro Nunes
Vida de Pedro Nunes
Astrónomos e cosmógrafos
contemporâneos de Pedro Nunes
Estado
de Portugal no século XVI
No segundo período da História da cultura das
Matemáticas em Portugal, em que vamos entrar, período
que coincide com o século XVI, está êste país no auge
da sua glória. O manto dos seus reis, a-pesar-dos
defeitos que cobre, deslumbra todo o mundo então
conhecido. A semente espalhada pelos seus antecessores do
século XV germinara e está produzindo frutos maduros
que aqueles estão colhendo. Nenhum país o excede em
fama e poderio. E êle um povo de eleição cujos
marinheiros navegaram em frágeis caravelas, hàbilmente
dirigidas, até à Índia, a Terra para eles da
Promissão, que lhe deu a glória de um povo de heróis,
e até ao Brasil, que lhe havia de dar no futuro a honra
de um povo colonizador.
Demais, a Providência, generosa para êste povo, não
lhe deu sòmente heróis na navegação e na guerra,
deu-lhe também heróis do pensamento: deu-lhe Camões, o
Homero das suas glórias, deu-lhe cronistas insignes,
para narrar os feitos na terra e no mar dos seus soldados
e marinheiros e, como presente apropriado ao seu papel
nos Oceanos, deu-lhe cosmógrafos eminentes, que
organizaram a ciência da navegação do seu tempo e
prepararam a ciência da navegação do futuro.
Abriu o período D. Manuel, monarca venturoso e
vaidoso, que teve a ventura de ver partir e regressar os
heróis que primeiro aportaram à Índia e pôde ter a
vaidade de ser o chefe supremo de tal gente.
Seguiu-se D. João III, que conservou e mesmo aumentou
os domínios que herdou de seu pai, mas que, pelo seu
espírito intolerante, ou talvez mal aconselhado, cometeu
o êrro nefasto de introduzir em Portugal e proteger a
sinistra instituïção do Santo Ofício.
Veio depois D. Sebastião, que, com a sua febre de
heroísmos, pretendendo ajuntar aos seus domínios e aos
domínios da cristandade as terras da Mauritânia,
sucumbiu com o exército português nos areais malditos
de Alcácer-Quivir.
Este terrível desastre feriu mortalmente Portugal, a
cuja agonia assistiu um velho decrépito, o Cardial D.
Henrique, que fechou fùnebremente a dinastia que
auspiciosamente abrira D. João I.
Depois as terras de Afonso Henriques, sagradas para os
Portugueses, caíram no domínio do ambicioso Filipe II
de Castela.
E assim sucumbiu miseramente uma nação que menos de
um século antes subira a uma glória épica que fora o
assombro do mundo. É que o manto real, quanto mais se
estendia, mais e maiores vícios e erros cobria, vícios
e erros que começaram a manifestar-se no reinado de D.
Manuel, aumentaram no reinado de D. João III e
continuaram a aumentar no reinado de D. Sebastião; por
isso aquele manto, depois de manchado de sangue na
Mauritânia, transformou-se em sudário da dinastia e do
reino.
Eis o cenário histórico em que vai passar-se o
segundo período da história da cultura das Matemáticas
em Portugal.
Álvaro Tomaz e
Gaspar Nicolas, aritméticos
No primeiro período da história das Matemáticas em
Portugal não apareceu cultor algum destas ciências que
se ocupasse de assuntos diferentes da sua aplicação à
náutica. Não aconteceu o mesmo no segundo. Aparece logo
a abri-lo um aritmético insigne, Álvaro Tomaz.
É êste matemático autor de uma obra intitulada Liber
de triplice motu, publicado em Paris em l509, e, pelo
que diz no prefácio, sabe-se que nasceu em Lisboa e que
foi professor em um colégio da capital da França.
Ainda há bem poucos anos era completamente
desconhecido em Portugal, segundo creio, e é ao ilustre
professor da Universidade de Madrid Rey-Pastor que
devemos a notícia dele, bebida em um excelente livro que
em 1926 consagrou à historia dos matemáticos espanhóis
do século XVI. Ocupou-se Álvaro Tomaz no livro
mencionado do movimento do ponto sôbre o plano e a sua
doutrina a êste respeito está estreitamente ligada à
que fôra dada por Oresme, no século XIII, no tratado De
latitudinibus formarum, onde êste célebre geómetra
estudara o movimento do ponto por meio da representação
sôbre um plano da relação entre a velocidade e o tempo
relativamente a dois eixos de coordenadas. Esta obra foi
comentada no século XIV por Biagio de Parma e era muito
conhecida nos tempos de Álvaro Tomaz.
No livro do matemático português, a teoria de Oresme
é estudada por um método aritmético-geométrico
engenhoso e dão-se nêle teoremas notáveis, entre os
quais assinalaremos o seguinte: em qualquer movimento
variado de um ponto, a linha descrita poderia ser
percorrida no mesmo tempo por outro ponto com velocidade
constante, compreendida entre a maior e a menor
velocidade do primeiro ponto; teorema que, aplicado ao
movimento variado, dá um resultado que se tem atribuído
a Galileu, mas que, segundo se vê em um excelente
trabalho de Marcolongo sôbre Leonardo de Vinci, fora
dado antes pelo mencionado matemático Oresme e
reproduzido em um manuscrito daquele célebre pintor e
sábio.
O livro de Álvaro Tomaz ainda notável pela
habilidade com que o autor soma nêle algumas séries
numéricas e pelo engenho com que determina limites para
o valor de outras que, por dependerem de logaritmos, se
não podiam somar naqueles tempos, e ainda de outras que
ainda agora se não sabem somar.
A intervenção das séries nas questões de
cinemática estudadas no livro considerado explica-se do
modo seguinte. No modo de estudar estas questões,
divide-se o tempo em intervalos em progressão
geométrica, considera-se como constante a velocidade do
movimento durante cada intervalo e consideram-se as
velocidades correspondentes aos diversos intervalos como
ligadas por uma lei. A soma dos espaços percorridos pelo
ponto durante os diversos intervalos é uma série com
lei determinada que o autor do livro estuda para diversas
hipóteses daquela lei. O movimento uniformemente variado
corresponde ao caso de velocidades em progressão
aritmética.
O livro de Álvaro Tomaz é muito raro; a Biblioteca
Nacional de Lisboa possui um exemplar recentemente
adquirido. Não nos foi possível obter qualquer
informação biográfica a respeito do autor;
provavelmente saiu cedo de Portugal, fêz os seus estudos
em França, e ali ficou a ensinar.

O livro mais antigo consagrado em Portugal à
Aritmética tem por título Tratado da pratica
Darismetica, e foi publicado pela primeira vez em
1519 e o seu autor chamava-se Gaspar Nícolas. Diz-se que
era natural de Guimarães.
Abre êste tratado por alguns capítulos sôbre as
regras para somar, subtrair, multiplicar e dividir
números inteiros e fraccionários, para extrair as
raízes quadradas dos números inteiros e para somar
progressões. Seguem-se depois numerosos problemas de que
o autor dá as soluções, empregando para isso a regra
de três, a regra de falsa posição, etc. Alguns dêstes
problemas são de utilidade na vida, outros são
interessantes curiosidades numéricas.
Percorrendo-o com atenção, nota-se que o livro
mencionado é um excelente manual de Aritmética
prática, muito claro e simples na exposição das
doutrinas, sem teorias, que certamente prestou bons
serviços no século XVI. Dá-lhe um interêsse especial
a circunstância de o autor do livro ter recolhido alguns
problemas considerados nas obras de Frei Lucas de Burgo,
como êle próprio diz, sendo assim talvez o primeiro a
fazer notar na nossa Península o célebre matemático
italiano que depois Marco Aurel, na Espanha, e
principalmente Pedro Nunes, em Portugal, engrandeceram,
ensinando as suas teorias algébricas.
Gaspar Nícolas não deduz no seu tratado as
soluções dos problemas que considera, não emprega a
arte algébrica; enuncia-os, indica as soluções e
verifica-as, sem dizer o modo como as obteve. É pena que
o mesmo aritmético não tenha extraído da obra de Frei
Lucas a parte relativa à Álgebra, para a fazer conhecer
em Portugal.
O livro de que acabamos de falar, foi muito lido em
Portugal no século em que foi escrito e nos seguintes,
porque, além da edição de 1519, da qual se conhece
apenas um exemplar, possuído pela Faculdade de Ciências
do Pôrto, teve outras em 1530, 1541, 1573, 1594, 1613,
1679 e 1716.
Na Espanha, antes de aparecer em Portugal o livro de
Gaspar Nícolas, tinham sido publicados os tratados de
Aritmética de Ciruelo, Frei João de Ortega e Siliceo.
Seria interessante comparar com eles os do aritmético
português, mas não me foi possível fazê-lo, por não
ter podido obter os tratados daqueles autores.

Os livros de Frei Lucas de Burgo e de Gaspar Nícolas
inspiraram outro aritmético português, Bento Fernandes,
na composição do seu Tratado da arte d'Arismetica,
publicado em 1555, para uso dos mercadores, livro que
contém, como o de Nícolas, as regras necessárias para
executar as operações numéricas e para resolver os
problemas que apareciam naqueles tempos no exercício do
comércio, e, além disso, as doutrinas de Frei Lucas
para a resolução das equações do primeiro e do
segundo grau. Este tratado representa pois um grande
progresso sôbre o de Nícolas, que não contém estas
últimas doutrinas, já então divulgadas na Espanha por
Marco Aurel.

Outro escritor dos mesmos tempos que se ocupou de
assuntos matemáticos estranhos à náutica foi D.
Francisco de Melo, Bispo de Goa. Estudou em França, onde
foi discípulo de Brissot, e, depois de voltar a
Portugal, compôs comentários em latim às doutrinas de
Óptica atribuídas a Euclides e ao tratado De
incidentibus in humidis de Arquimedes, que ficaram
inéditos.
Pedro Nunes como
cosmógrafo
Voltemos à história da Astronomia náutica,
interrompida para poder apresentar alguns aritméticos,
sem alterar a ordem cronológica. Entra em cena Pedro
Nunes e, com êle, a hegemonia das Matemáticas na
Península ibérica vai passar da Espanha para Portugal.
Não devemos todavia esquecer que no período em que
vamos entrar, teve o país vizinho em Frei João de
Ortega um aritmético ilustre, cujo valor foi assinalado
com elogio pelo sr. Rey-Pastor no seu já mencionado
livro sôbre os matemáticos espanhóis do século XVI.
Como dissemos nos Panegíricos e Conferências,
Pedro Nunes apareceu na cena do mundo no alvorecer da
civilização moderna, quando Portugal estava no período
do seu máximo esplendor. Poucos anos antes de nascer,
tinha Cristóvão Colombo descoberto a América, Vasco da
Gama o caminho marítimo da Índia e Pedro Álvares
Cabral o Brasil. No ano em que nasceu, 1502 fêz Vasco da
Gama a sua segunda viagem à Índia. Estava em plena
juventude quando se realizou a primeira circunnavegação
do mundo.
«Foi pois educado a ouvir falar das glórias
lusitanas e isto não podia deixar de influir para lhe
levantar o espírito, que era por natureza bem dotado, e
talvez mesmo para fixar a direcção em que havia de
exercer a sua actividade científica.
«De facto, em 1529 foi chamado a desempenhar as
funções de Cosmógrafo do Reino. Era nessa ocasião
Bacharel em Medicina pela Universidade portuguesa, então
instalada em Lisboa, e tinha visitado em romaria de
estudo a Universidade de Salamanca, que era naqueles
tempos o Santuário da ciência hispânica; mas abandonou
logo aquela ciência, então cheia de quimeras
astrológicas, que não poderiam satisfazer o seu
espírito são, para se entregar completamente aos
estudos de assuntos sólidos de Matemática e Física,
começando, para cumprir os deveres do seu cargo, por
aqueles que interessavam especialmente à Náutica».
Como dissemos, também no livro mencionado, .quando foi
nomeado Cosmógrafo do Reino, tinham terminado as grandes
descobertas geográficas dos portugueses, mas estava em
plena actividade a exploração das riquezas das terras
por êles descobertas. Estava-se no tempo em que
Portugal, para consolidar e utilizar os seus domínios no
Oriente, procurava espalhar feitorias e missões
religiosas pelos lugares mais apropriados para aquele
fim; em que os seus soldados se batiam heroicamente com
os árabes, que pretendiam conservar nas suas mãos o
comércio da Índia; em que entre Lisboa e Calecute
navegavam numerosas naus, que traziam a Lisboa as
riquezas do Levante, fazendo desta cidade a rainha dos
mares e o centro do comércio do mundo».
Começava-se também na mesma época a prestar
atenção ao comércio e navegação do Brasil, cuja
civilização havia de ser mais tarde, como já dissemos,
honra de um povo de colonizadores, como as conquistas da
Índia foram glória de um povo de heróis. Foi com
efeito nos primeiros anos depois que Pedro Nunes começou
a exercer as funções de cosmógrafo que Martim Afonso
de Sousa, fundando no Brasil as primeiras colónias que
Portugal teve na América, deu os passos iniciais para a
formação do nosso extenso império do Ocidente.
A colonização da África começou mais tarde e dá
também honra aos Portugueses. Mas, ao abrir o século
XVI, tôda a costa do então misterioso continente, a
oriente e ocidente tinha sido visitada por nautas lusos e
o tormentoso Cabo da Boa Esperança era já o monumento
levantado na história a glória de Bartolomeu Dias, que
primeiro o tinha descoberto e nas águas do seu mar
perdera a vida.
O que era nesses tempos o império português no
oriente di-lo eloqüentemente o grande cosmógrafo em uma
das suas obras:
«Não há dúvida que as navegações deste reino, de
cem anos a esta parte, são as maiores, mais
maravilhosas, de mais altas e mais discretas conjecturas
que as de nenhuma outra gente do mundo. Os portugueses
ousáram cometer o grande mar Oceano. Entraram por êle
sem nenhum receio. Descobriram novas ilhas, novas terras,
novos mares, novos povos, e, o que mais é, novo céu e
novas estrêlas. E perderam-lhe tanto o medo, que nem a
grande quentura da torrada zona, nem o descompassado frio
da extrema parte do sul, com que os antigos escritores
nos ameaçavam, lhes pôde estorvar que, perdendo a
Estrêla do Norte e tornando-a a cobrar, descobrindo e
passando o temeroso Cabo da Boa Esperança, o mar da
Etiópia, da Arábia e da Pérsia, puderam chegar à
Índia. Passaram o rio Ganges, tão nomeado, a grande
Trapobana e as ilhas mais orientais. Tiraram-nos muitas
ignorâncias e mostraram-nos ser a terra maior do que o
mar, e haver antípodas, do que até os santos duvidavam,
e que não há região que nem por quente nem por fria se
deixe de habitar. E que, em um mesmo clima e a igual
distância do Equador há homens brancos e pretos e de
mui diferentes qualidades. E fizeram o mar tão chão que
não há quem hoje ouse dizer que achasse novamente
alguma pequena ilha, alguns baixos ou sequer algum penedo
que por nossas navegações não seja já descoberto».
Este hino caloroso à gloria dos portugueses foi
ouvido por Camões, que, com o alto pensamento que tais
palavras exprimem, compôs a grandiosa epopeia dos feitos
da gente lusa na terra e no mar.

Passemos agora a considerar as obras em que Pedro
Nunes se ocupou da ciência e arte de navegar.
Para cumprir os deveres do seu cargo, começou o nosso
cosmógrafo por publicar, em 1537, um livro precioso com
os artigos seguintes: 1.º Tratado da Esfera; 2.°
Teoria do movimento do Sol e da Lua; 3.° Tratado de
Geografia de Ptolomeu; 4.° Tratado de algumas duvidas da
navegação; 5.° Tratado em defensam da carta de marear;
livro, que por ser hoje muito raro e procurado, foi
incluído por Joaquim Bensaúde na sua colecção de
documentos foto-gravados para a história das
navegações marítimas.
Os três primeiros tratados são traduções do latim
em português de obras de Sacrobosco, Purbachio e
Ptolomeu.
Já dissemos que João de Sacrobosco tinha composto em
latim no século XIII um tratado De sphera. Este
livro ainda muito usado no século XVI em tôda a Europa
como texto de iniciação para o estudo da Cosmografia,
era uma exposição de doutrinas desta ciência,
inspirada principalmente pelos livros de Ptolomeu e de
alguns astrónomos árabes, insuficiente sob o ponto de
vista matemático, mas muito simples, clara e elementar,
sob o ponto de vista descritivo, e por isso muito
apropriada aos médicos-astrólogos e aos pilotos. Por
ser útil aos astrólogos teve muita aceitação, e, por
ser útil aos pilotos as passagens que êstes precisavam
conhecer, tinham já sido publicadas em tradução
portuguesa nas edições do Regimento do astrolabio
anteriormente mencionadas e no livro sôbre náutica de
Francisco Faleiro, também já mencionado. Pedro Nunes
traduziu-a tôda e enriqueceu-a com Notas que a
valorizaram muito.
Pode estranhar-se que o nosso cosmógrafo, na sua
tradução deste livro não cite o nome do autor e
também que o não tenham citado os cosmógrafos
portugueses que dêle tinham extraído resumos.
Certamente consideravam a obra do célebre monge como
simples modêlo clássico, assás espalhado, por ter sido
muito divulgado em numerosas edições, cuja redacção
aproveitaram, mas cujo pensamento era de Ptolomeu.
Também pelo mesmo motivo no segundo dos tratados
mencionados não citou Purbachio.
Entre as Notas juntas por Nunes ao Tratado da
esfera há uma, que foi traduzida em latim por Elia
Vineto e junta a algumas edições da obra de Sacrobosco
que se publicaram depois, Nota em que o nosso matemático
revelou pela primeira vez originalidade de espírito e
habilidade no emprego dos métodos sintéticos dos
geómetras helénicos, demonstrando e generalizando uma
observação de Sacrobosco sôbre climas.
Ptolomeu, no Almagesto (Parte II, Cap. VI) e no
Tratado de Geografia (Parte I, Cap. X) tinha
dividido a parte da Esfera terrestre compreendida entre o
Equador e o Círculo polar ártico em zonas tais que nos
paralelos que limitam cada zona a diferença de duração
do maior dia do ano é de meia hora para as mais
próximas do Polo e de um quarto de hora para as outras
(procurando com esta distinção evitar zonas
excessivamente largas nas vizinhanças do Equador e
outras excessivamente estreitas na vizinhança do
Círculo polar) e tinha determinado as latitudes dos
paralelos que limitam cada zona. Sacrobosco reduziu a
doutrina de Ptolomeu considerando sòmente a parte da
Terra que no seu tempo se julgava habitável e nela sete
zonas tais que a diferença da duração do dia no maior
dia do ano era de meia hora e verificou numèricamente
que a altura destas zonas diminui quando se aproximam do
Polo. Estas sete zonas são as que na Geografia antiga se
chamavam climas e a observação que a respeito da
variação da sua largura faz Sacrobosco poderia ter sido
sugerida pela divisão que, como dissemos, Ptolomeu faz
das suas zonas em grupos correspondentes a meia hora e a
um quarto de hora de diferença da duração do maior dia
do ano nos paralelos que limitam cada uma.
Ora, Pedro Nunes deu forma matemática geral a esta
doutrina e obteve assim o teorema seguinte:
A zona compreendida entre dois paralelos
terrestres, situados do mesmo lado do Equador, tais que a
diferença das durações de um mesmo dia qualquer nestes
paralelos tenha um valor arbitràriamente dado diminui em
largura, quando a zona se aproxima do Polo correspondente
da Terra.
Na Nota consagrada ao teorema de que acabamos de
falar, demonstrou ainda o nosso cosmógrafo uma regra
geométrica, uma construção gráfica e um método
mecânico para determinar a duração de um qualquer dia
do ano em um lugar dado da Terra.
Tudo isto merece ser notado, porque é obtido por
considerações planimétricas feitas sôbre uma figura
que está situada no plano do meridiano e sôbre outra
que está situada no plano de um paralelo e é rebatida
sôbre aquele plano, oferecendo assim um exemplo
interessante de um método clássico de Geometria
descritiva moderna.
Convém, todavia, observar que êste método dos
rebatimentos tinha já sido empregado em outras questões
por Ptolomeu, nos Analemma, e por alguns
Geómetras árabes.
Delambre, referindo-se na sua História da Astronomia
à Nota que acabamos de assinalar, diz que a
demonstração de Pedro Nunes do teorema mencionado não
merece ser conservada e substitui-a por uma prova
trigonométrica. Nós pensamos, pelo contrário, que
aquela demonstração constitui um exemplo interessante
de síntese geométrica, com sabor helénico, e que,
sendo traduzida em estilo moderno, não é mais complexa
do que a de Delambre.

Passemos a considerar os escritos em que Pedro Nunes
se ocupou especialmente da ciência e arte da
navegação.
Os títulos dêstes escritos são: 1.° Tratado
sobre certas duvidas da navegação, já mencionado;
2.° Tratado em defensam da carta de marear,
também já mencionado; 3.° De arte atque ratione
navigandi.
Diz o autor dêstes escritos no segundo dêles que
nenhuma regra que tenha fundamento na parte especulativa
ou técnica pode ser bem praticada e entendida sem
notícia daqueles princípios em que se funda, porque de
outra sorte os que dela usassem fàcilmente se
enganariam.
A exposição dêstes princípios, pelo que respeita a
Náutica, é o objecto dos tratados cujos títulos
acabamos de mencionar.
O último, isto é, o tratado De arte atque ratione
navigandi , é o mais importante dêles e mesmo
talvez dos que, antes da morte de Nunes, se escreveram
sôbre a ciência e arte da navegação.
Algumas das doutrinas expostas neste tratado são a
reprodução das que tinha dado nos outros dois, outras
são nêle estudadas pela primeira vez; mas aquelas são
apresentadas sob forma mais científica. Nos trabalhos
primeiramente escritos vê-se o cosmógrafo a ensinar
doutrinas de náutica aos pilotos portugueses, no último
vê-se o sábio a divulgar as suas investigações entre
os homens cultos de todos os países que se interessavam
por aquelas doutrinas. Por isso escreveu os primeiros em
português e o último em latim. Nos primeiros tratados
revelam-se os primeiros alvores do espírito científico
do grande cosmógrafo; no último mostra-se êste
espírito em todo o seu brilho a constituir a ciência da
navegação do seu tempo e a preparar a do futuro.
Vejamos agora as questões principais estudadas nos
três livros.
Na navegação daquele tempo obrigava-se o navio a
seguir na superfície do mar uma trajectória tal que o
ângulo da direcção do movimento com o meridiano se
conservasse constante. A esta curva dava-se então o nome
de linha do rumo e dá-se hoje o nome de loxodromia.
A direcção do meridiano era dada aproximadamente pela
agulha magnética da bússola.
Julgavam os pilotos e estava mesmo escrito na Arte
de marear de Faleiro que as linhas de rumo coincidem
com círculos máximos da Esfera terrestre.
Ora, Pedro Nunes mostrou que as linhas de rumo são
geralmente espirais esféricas que dão um número
infinito de voltas à roda dos Polos da Terra e que as
únicas linhas de rumo circulares são os meridianos e os
paralelos, que correspondem evidentemente aos ângulos de
rumo de zero e de noventa graus. E ajuntou ainda,
colocando-se no ponto de vista histórico, que a não
coincidência em geral das linhas de rumo com círculos
da Esfera terrestre tinha já sido notada por Ptolomeu,
apoiando-se para isso em duas passagens do Tratado de
Geografia do grande astrónomo de Alexandria.
Na primeira destas passagens, o autor delas, para
obter a menor distância, isto é, a distância por
círculo máximo entre Corura e Palura, na Índia, abate
à distância medida, navegando entre as duas cidades, a
têrça parte desta distância, para a corrigir dos
rodeios do navio, isto é, segundo Pedro Nunes, do
excesso do comprimento do arco da linha de rumo sôbre o
arco do círculo máximo cujo comprimento se procurava;
na segunda passagem, o mesmo astrónomo, querendo obter o
comprimento do arco do paralelo compreendido entre
Chersoneso e Zabas, terras situadas na mesma latitude,
não faz correcção alguma ao resultado da medida, por
serem, diz Nunes, todos os paralelos linhas de rumo.
Esta explicação das referidas passagens é
interessante e não improvável, mas a primeira passagem
é tão vaga, que não podemos ter a certeza de que tal
explicação represente o pensamento de Ptolomeu. Mas se
o grande astrónomo alexandrino pensou na natureza da
curva de rumo, o seu alto espírito geométrico não a
confundiu com círculos.
O que podemos dizer com segurança é que Pedro Nunes
trouxe a dita curva do campo da náutica empírica, em
que era para os pilotos apenas a rota descrita pelo navio
dirigido pela bússola, para o campo da Geometria para
onde é a curva descrita por um ponto que corta os
meridianos da esfera sob um ângulo constante, que
mostrou que não é geralmente circular e que abriu a sua
teoria.
Os cosmógrafos portugueses que o precederam,
conheciam um processo para determinar a diferença das
longitudes de dois pontos da curva com uma aproximação
tanto maior quanto menor fôsse a sua distância; e, por
meio de aplicações dêste processo a arcos parciais em
que decompunham um arco dado da curva, obtinham a
diferença de longitudes dos pontos que o limitam com
aproximação tão grande quanto queriam.
Este processo equivale ao emprêgo da equação da
curva. Esta equação, obtida mais tarde por Leibniz,
depende de logaritmos, algoritmo desconhecido no tempo de
Nunes, e a vantagem que teria o emprêgo desta equação
sôbre o método usado nas nossas antigas navegações
para resolver o problema considerado, seria o de reduzir
o cálculo numérico que exige ao cálculo por
logaritmos.
E acrescentemos ainda que os cosmógrafos mencionados
conheciam ainda um modo de obter o comprimento dos arcos
da linha de rumo com aproximação tão grande quanto se
queira.
Para se aplicarem estas doutrinas à navegação,
continham os regulamentos mencionados na Primeira Parte
dêste livro duas tábuas numéricas que davam, uma a
diferença de longitudes de dois lugares da curva
percorrida pelo navio correspondentes à diferença de um
grau em latitude, a outra o comprimento dêste arco. Ora,
Pedro Nunes refez, na segunda das obras mencionadas,
estas tábuas, melhorando-as e inventou um instrumento, a
que chamou compasso e que adiante descreveremos, para
medir a razão do arco do paralelo terrestre
correspondente a uma latitude dada para o raio da Terra,
razão que é necessário conhecer para se aplicar a
primeira tábua.
Esclareceremos numa Nota, no fim dêste volume, o que
acabamos de dizer sôbre a linha de rumo, empregando o
simbolismo algébrico.
Convém assinalar aqui, ao terminar esta doutrina, o
facto que levou Pedro Nunes a considerar a linha de rumo,
facto notado por êle próprio no Tratado sobre certas
duvidas da navegação.
Martim Afonso de Sousa, fundador das primeiras
colónias que Portugal teve no Brasil, querendo, na sua
volta da América, vir do Rio da Prata a Lisboa, tomou e
conservou o rumo de leste, julgando que assim seguiria o
círculo máximo perpendicular ao meridiano do lugar da
partida e que iria encontrar o Equador num dos pontos em
que aquele círculo o cortava. Notou porém com
surprêsa, passados alguns dias, que, em vez de se
aproximar do Equador, ia seguindo o paralelo do lugar da
partida. O motivo do êrro do navegador está em admitir
que as linhas de rumo coincidem com os círculos máximos
da esfera terrestre e o motivo de seguir o paralelo do
lugar de partida está na coincidência dos paralelos com
as linhas de rumo correspondentes ao ângulo de 90.°.
São estas as explicações que Nunes deu do facto
narrado.
Voltou Pedro Nunes a ocupar se da linha de rumo no
segundo dos livros mencionados a propósito da sua
representação nas cartas náuticas, como veremos, mas
só no terceiro tratado se deteve a estudá-la,
apresentando nêle algumas propriedades expressas por
desigualdades, relativas à variação do comprimento dos
seus arcos com as longitudes e latitudes das
extremidades, e ocupando-se da sua forma, do seu uso na
náutica, do modo de as traçar na esfera, etc.

No tratado De arte atque ratione navigandi,
apresentou Pedro Nunes um modo de navegar por arcos de
círculo, representável matemàticamente, do qual a
navegação pela linha de rumo é um caso limite.
A-pesar-dêste método não ter interêsse prático,
julgamos dever apresentá-lo aqui, por motivos que depois
se verão. Um caso particular tinha já sido considerado
pelo seu autor no Tratado de certas duvidas na
navegação para explicar o modo de navegar por um
paralelo da Terra.
Supõe o autor que o navio segue uma linha formada por
uma série de arcos de círculos máximos tais que os
ângulos que fazem com os meridianos nas primeiras
extremidades sejam iguais e tais que sejam também
iguais, mas de grandeza diferente da daqueles, os
ângulos que fazem os mesmos arcos com os meridianos nas
segundas extremidades.
A curva de rumo é o limite para que tende aquela
linha, quando a diferença dos ângulos nas duas
extremidades tende para zero.
Para se apreciar êste método, diz o autor, convém
notar que um navio não segue no mar rigorosamente uma
linha de rumo, porque a agulha magnética vai fazendo
pequenos desvios sucessivos para um e outro lado, que o
marinheiro que maneja o leme, vai corrigindo. Segue uma
série de arcos de círculos máximos que formam uma
linha quebrada que se aproxima tanto mais da curva do
rumo, quanto menores são aqueles desvios. Nunes, para
tratar a questão matemàticamente, supõe todos os
desvios iguais e no mesmo sentido.
Por cálculos simples, que não exporemos aqui, mas
que serão apresentados em Nota no fim dêste livro,
mostra-se que, se um navio parte de um lugar com rumo
dado e vai seguindo uma série de arcos de círculo nas
condições mencionadas, podem determinar-se pela
Trigonometria esférica as coordenadas geográficas das
posições que vai ocupando e os comprimentos dos arcos
percorridos.
O nosso cosmógrafo dá-nos pois assim um novo modo de
navegar, bem determinado, em que o nauta segue próximo
da linha de rumo, quando a distância percorrida não é
grande.
Este método foi considerado como inexacto por Simão
Stevin e esta apreciação foi reproduzida por Montucla
na sua Histoire des Mathématiques e depois em
Portugal por Garção Stockler, no seu Ensaio
histórico, e Rodolfo Guimaráes, no artigo que, a
respeito de Nunes, publicou nos Anais científicos da
Academia Politécnica do Pôrto. Nós pensamos que as
censuras do célebre geómetra de Bruges não são
aplicáveis à doutrina de Pedro Nunes e que esta
doutrina é exacta; o que aquele matemático poderia
dizer é que não é prática.
Vejamos o que diz Stevin. Este geómetra aplica a
doutrina de Nunes ao cálculo do comprimento do arco de
uma linha de rumo que parte do Equador com um ângulo de
45º e que termina cêrca de 10° abaixo do Polo e,
comparando o número assim obtido com o que dá outro
método, especial para êste caso por êle imaginado,
conclui que o número obtido pelo método do matemático
português dá o comprimento procurado com aproximação
insuficiente. Ora, isto não mostra que a doutrina de
Pedro Nunes é falsa, mas sim que não é suficientemente
aproximada para arcos tão grandes.
Indo mais longe do que Stevin, Stockler diz que certas
equações que Nunes empregou, são incompatíveis com
outras tiradas da equação leibniteziana da curva de
rumo (ver a Nota no fim do livro). Isto é exacto, mas
estas últimas equações e as de Nunes correspondem a
questões diversas.
As equações de Nunes correspondem a linhas formadas
por séries de arcos de círculo convenientemente
escolhidos, de que as linhas de rumo são limites, e as
outras correspondem a estas últimas linhas.
Ajuntemos que Stevin propôs, para substituir a
doutrina de Nunes, uma outra doutrina que não difere
essencialmente da que fôra já empregada no século XV
pelos pilotos portugueses e se encontra no Regimento
do astrolábio, mencionado na Parte Primeira
dêste livro, como se verá nas Notas.
Ajuntemos ainda que esta doutrina é aplicada por
Stevin de um modo que não convém. Em quanto que na
aplicação dela os nautas portugueses fazem depender o
cálculo das longitudes do valor das latitudes, que se
obtinham fàcilmente por meio do astrolábio, Stevin,
invertendo o problema, faz depender o cálculo das
latitudes do valor das longitudes, que, antes da
invenção dos cronómetros, não eram fáceis de medir.
Pedro Nunes iludiu-se em quanto ao valor da sua
doutrina como meio prático de resolver o problema da
navegação pela linha de rumo. Qual foi o motivo desta
ilusão? Vamos tentar explicá-lo.
Como dissemos, empregava-se na náutica para resolver
êste problema um método que equivale a considerar a
curva de rumo como um polígono de lados tão pequenos
quanto se queira. Ora, provàvelmente o nosso
matemático, notando que às linhas rectas do plano
correspondem na esfera círculos máximos, entendeu que,
substituindo aquele polígono por uma linha composta de
arcos dêstes círculos dispostos do modo que apresentou,
se aproximava mais da linha de rumo do que por meio
daquele polígono. Mas deu-se o contrário porque
enquanto que o polígono tem os seus vértices sôbre a
curva, os vértices da linha que substitui a esta curva
estão fora dela. Abriu pois apenas uma teoria que não
teve seguimento porque a descoberta por Leibniz, por meio
da antiga teoria da curva, da sua equação esférica,
expressa por logaritmos, tornou a nova doutrina inútil.

Ocupou-se também Pedro Nunes nas obras consagradas à
náutica da navegação por círculo máximo, dando a
relação que deve ligar a latitude com o rumo em cada
ponto dêste círculo e dando uma regra prática para se
obter o efeito desejado por meio de observações das
latitudes tão freqüentes quanto seja possível. As
regras que actualmente se empregam neste problema de
navegação, isto é, na ciência da navegação
ortodrómica, coincidem com as dadas por Pedro Nunes,
mas os livros que se ocupam delas não mencionam o nome
de quem primeiro estudou o dito problema(l).
(1) Veja-se no fim
dêste volume uma Nota, onde são dadas a
relação e a regra mencionadas.
|
Com a doutrina da linha de rumo está
estreitamente ligada a da carta náutica, de que Pedro
Nunes se ocupou com muito desenvolvimento, ainda que de
um modo não completamente satisfatório no Tratado em
defensam da carta de marear e no tratado De arte
atque ratione navigandi.
O nosso matemático pôs nestes tratados nitidamente
as condições a que estas cartas devem satisfazer, para
serem um instrumento matemático aplicável à
determinação do rumo a seguir de um lugar a outro.
Estas condições são: representar por linhas rectas as
linhas de rumo; conservar os ângulos que estas linhas
fazem com os meridianos.
Como os meridianos e os paralelos são linhas de rumo,
resulta em particular destas condições que aqueles
círculos devem ser representados nas cartas por dois
sistemas de rectas paralelas, sendo as de um sistema
perpendiculares as do outro. Está neste caso a carta
chamada quadrada, adoptada nas navegações
portuguesas, da qual já falámos na Primeira Parte deste
livro.
O nosso matemático, aprovando a escolha ocupou-se
largamente dela em um dos escritos mencionados, onde deu
conselhos aos pilotos para a usarem bem e a defendeu de
censuras que alguns lhe faziam, censuras em que algumas
vezes tinham razão, porque a carta lhes não dava tôdas
as informações de que careciam para dirigir as naus com
segurança, e algumas vezes êle próprio mais a atacou
do que defendeu.
Esta carta tinha com efeito dois graves defeitos: 1.°
deformava excessivamente a superfície da Terra, fazendo
todos os paralelos iguais e, representando-a assim como
cilíndrica; 2.° não eram nela representadas por linhas
rectas as curvas de rumo, exceptuando os meridianos e os
paralelos.
Para remediar estes defeitos, o nosso cosmógrafo,
imitando o que tinham feito outrora Marino de Tiro e
Ptolomeu para os mapas de regiões terrestres, recomenda
que se substitua a carta geral da Terra por uma série de
cartas de zonas, tomando em cada zona para base da
superfície cilíndrica que a substitui, o paralelo
médio da zona e dando à zona uma altura maior ou menor,
segundo o grau de aproximação com que se queira
representá-la. As linhas de rumo da zona são então
substituídas no cilindro por hélices, a que
correspondem na carta, que é a planificação do
cilindro, linhas rectas. Recomenda depois que se reúnam
tôdas estas cartas parciais em um livro.
Mas êste remédio tem ainda um grave inconveniente:
não dá as ligações entre os lugares das diversas
zonas.
O matemático português parou aqui. Não se lembrou
de reünir todas as cartas parciais em uma carta única e
dar a tôdas a mesma largura, para o que bastaria
empregar no traçado relativo a cada zona uma escala
especial convenientemente escolhida. Por não se lembrar
disto, deixou ao cartógrafo flamengo Gerardo Mercator a
honra da descoberta da carta rectangular reduzida,
com que se resolveu definitivamente o problema da carta
náutica, descoberta de que Nunes esteve bem perto.
O sistema de cartas planas primitivo era imperfeito, e
por isso os pilotos tinham dificuldade em o aplicar, e,
ao ler-se a defesa que dêle fêz Pedro Nunes, nota-se a
imprecisão que ordinàriamente acompanha a explicação
de doutrinas imperfeitas.
A-pesar porém dos seus defeitos a velha carta, com o
acrescento da representação dos rumos, referidos a
várias origens, prestou grandes serviços nas
navegações dos séculos XV e XVI. Com efeito, esta
carta satisfaz aproximadamente às condições
gerais indicadas por Nunes, quando representa uma zona da
Terra de pequena altura, de um lado e do outro do
Equador; e, quando se estende fora dos limites em que a aproximação
é suficiente, para poder representar o papel de
instrumento matemático na determinação a seguir pelo
navio de um lugar a outro, continua ainda a servir como
registo empírico de rumos e latitudes relativos a
lugares pertencentes a caminhos directamente percorridos
pelos pilotos.
É justo acrescentar que Nunes pôs nitidamente o
problema da carta e que, com as suas considerações
sôbre ele, preparou a descoberta de Mercator.
Voltaremos a ocupar-nos da carta náutica em uma Nota
no fim dêste livro, onde justificaremos matemàticamente
o que acabamos de dizer.
Antes de terminar esta doutrina das cartas náuticas,
devo observar que Pedro Nunes foi quem primeiro empregou
o sistema de representação planimétrica da superfície
da esfera atribuída a Sanson e conhecido pela
designação de carta de Flamesteed.
Fizemos notar êste facto no nosso Elogio
histórico do nosso geómetra publicado nos Panegíricos
e Conferências. Neste sistema de representação da
Terra, a cada lugar corresponde no plano um ponto cujas
coordenadas são o arco que mede no paralelo do lugar,
rectificado, a sua longitude e o arco que mede no
meridiano, também rectificado, a sua latitude, referidas
a dois eixos rectangulares, que representam o Equador e o
Primeiro Meridiano.
Ora, êste modo de representação foi indicado por
Nunes no Tratado em defensam da carta de marear,
onde mostrou também, indirectamente, que neste sistema
os meridianos da Terra são representados por curvas que
gozam da propriedade que define as curvas actualmente
chamadas linhas dos senos, como se verá em uma
das Notas da presente obra. Mais tarde Flamesteed
reinventou êste sistema de carta e aplicou-o aos mapas
geográficos.
Agora, terminada esta notícia dos trabalhos de Pedro
Nunes sôbre as cartas náuticas, seria oportuno falar
dos cartógrafos mais notáveis do século XVI; mas
dispensa-nos dêste trabalho a publicação recente de um
precioso livro de Armando Cortesão, intitulado Cartografia
e cartógrafos dos séculos XV e XVI, onde êste
assunto é estudado com desenvolvimento e documentação
abundante.
Quem conhece a história das navegações dos Lusos
supõe que nos arquivos portugueses e estrangeiros devem
existir muitas cartas náuticas do século XV. Engana-se;
são pouquíssimas as que têm sido assinaladas e muitas
delas estão perdidas.
Pelo contrário, são numerosas as cartas que se
conhecem do século XVI. O erudito autor do livro
mencionado enumera as cartas anteriores ao século XVII,
classifica-as, examina as que merecem ser examinadas,
compara as que convém que sejam comparadas, dá notícia
de algumas perdidas que ficaram registradas na história
da náutica, biógrafa os cartógrafos que compuseram as
principais (os Reineis, os Homens, Vaz Dourado, etc.) e
nota, como resultado dos seus estudos, «que a quási
totalidade das cartas daqueles tempos, ou são
genuinamente portuguesas, ou feitas sôbre dados
portugueses».
E agora, antes de terminar, ajuntaremos, recordando o
Visconde de Santarém, que o sr. Cortesão actualiza e
ordena as indagações daquele ilustre fundador da
história da cartografia portuguesa e avança muito no
caminho que êle abriu.

O problema da determinação das latitudes, sendo
fundamental na aplicação da Astronomia à Náutica,
não podia deixar de chamar a atenção de Pedro Nunes.
Começou por examinar as oito regras dadas no Regimento
do astrolábio para se obter por meio da altura da
Estrêla polar em oito das suas posições à roda do
Polo, a latitude do lugar da observação, regras a que
já nos referimos. Os números que figuram nestas regras
tinham sido obtidos por observações feitas em Lisboa e
os cosmógrafos julgavam que eram aplicáveis a todos os
lugares. Ora Nunes mostrou no tratado De arte atque
ratione navigandi que, quando a Estrêla polar está
fora do meridiano do lugar da observação, aqueles
números variam com a latitude dêste lugar, e por isso
manda abandonar as regras correspondentes às
observações extra-meridianas da referida Estrêla e
recorrer sòmente às observações das suas passagens
pelo meridiano.
Simplificou as regras dadas no mencionado Regimento
para a determinação das latitudes por meio da
observação da altura meridiana do Sol, modificando para
isso o modo de graduar o limbo do astrolábio. Tomava
para origem da graduação o ponto mais alto dêste limbo
e punha a nonagésima divisão no seu braço horizontal,
medindo assim directamente distâncias zenitais do Sol em
vez de alturas, e, fazendo as notificações
correspondentes nas regras para das observações deduzir
as latitudes, obteve outras de aplicação mais simples
do que as que tinham dado José Vizinho e Duarte Pacheco,
mas menos simples do que as que dera João de Lisboa.
Estas últimas correspondem, como já dissemos, a um modo
de graduar o limbo do astrolábio que nunca foi adoptado.
Deu, finalmente, um meio de determinar as latitudes
por observações da altura e azímute do Sol em qualquer
hora do dia.
Este azímute era obtido por meio de um instrumento de
sombra, aperfeiçoamento do que dera Francisco Faleiro,
instrumento que se reduzia a um prato horizontal
quadrado, no centro do qual estava um estilete vertical,
e a uma agulha magnética colocada em uma cavidade do
prato, circular e graduada, dividida ao meio pelo
diâmetro que passa pela origem da divisão.
Determinava-se por meio dêste instrumento
primeiramente o azímute do Sol relativamente ao
meridiano magnético, dado pela agulha, e corrigindo-o
depois da declinação magnética, que o instrumento
também dava, obtinha-se o azímute relativo ao meridiano
astronómico.
Para determinar depois a latitude do lugar da
observação, não recorre o nosso cosmógrafo a
cálculos numéricos. Resolve a questão muito
engenhosamente por meio de um traçado gráfico feito
sôbre uma esfera, onde estão descritos um círculo
máximo, que representa o horizonte, e outro, não
graduado, que passa pelo ponto que corresponde ao
zénite, traçado que determina os pontos da esfera que
correspondem aos Polos da Terra. Basta para isso, ajustar
sôbre a esfera um anel graduado que gire à roda dos
pontos que representam o zénite e o nadir. Tomando
sôbre o círculo que representa o horizonte, a partir do
círculo vertical traçado na esfera, um arco igual ao
azímute do Sol, levando o anel à extremidade dêste
arco e marcando por meio dêle no círculo vertical que
passa por êste ponto, um arco igual à altura do Sol,
medida pelo astrolábio, obtém-se um ponto cuja
distância por círculo máximo aos polos deve ser igual
ao complemento da declinação do Sol no dia da
observação. Tomando pois um compasso de pontas curvas e
traçando com uma abertura igual ao arco da esfera que
representa êste complemento da declinação, uma
circunferência sôbre a esfera, os dois pontos em que
corta o círculo nela traçado que passa pelo zénite,
determinam os pontos correspondentes aos Polos da Terra.
Os arcos que os unem ao ponto que representa aquele
zénite podem ser medidos pelo círculo graduado móvel.
Um dêstes arcos representa o complemento da latitude do
lugar. Para a escolha em cada caso, dêste arco, deu
Nunes um Regimento, em que considera as diversas
posições relativas do Sol e do observador.
Deu ainda Pedro Nunes outro método para determinar as
latitudes por meio de observações da altura e do
azímute, referido ao meridiano magnético, em duas
posições do Sol, que dispensa o conhecimento da
declinação magnética no lugar da observação e um
terceiro método para as determinar por meio de três
observações dos mesmos elementos em três posições,
que dispensa o conhecimento da declinação magnética e
da declinação do Sol no dia das observações.
Os métodos dados por Pedro Nunes para determinar as
latitudes por meio das alturas extra-meridianas do Sol, a
que acabamos de nos referir, foram publicados no Tratado
em defensam da carta de marear e no tratado De
arte atque ratione navigandi. São todos
teòricamente exactos e muito interessantes, mas
infelizmente não dão na prática resultados
suficientemente aproximados, por motivo de dificuldades
da sua aplicação. A sua insuficiência na prática foi
reconhecida por D. João de Castro, que os experimentou
nas suas viagens no Mar das Índias e no Mar Vermelho,
empregando para isso instrumentos que, ao partir de
Lisboa lhe foram oferecidos pelo Infante D. Luiz, filho
de D. Manuel, seu condiscípulo nas lições dadas por
Pedro Nunes no Paço real.
É estranhável que o nosso cosmógrafo não tenha
notado que, para os usos da náutica, só são
apropriados os métodos que dão a latitude por meio de
uma única observação, ràpidamente feita, evitando-se
assim os erros provenientes dos movimentos de oscilação
e avanço do navio e de um avanço durante as
observações. A esta causa de êrro juntavam-se, na
aplicação dos métodos mencionados, os defeitos de
construção e de funcionamento do instrumento empregado
para passar das observações para o valor das latitudes,
erros cuja importância só pode ser conhecida depois das
aplicações que D. João de Castro fêz dêle. Os
métodos de Nunes caíram diante das observações dêste
grande navegador, mas na queda salvou-se o engenho do
insigne teórico, que primeiro dotou a Astronomia com um
método para determinar as latitudes por observações
extra-meridianas do Sol.
Mais tarde, depois da invenção dos cronómetros,
puderam empregar-se nesta questão os ângulos horários
do Sol que estes instrumentos determinam, em vez dos seus
azímutes, e assim subiu se, aproveitando os progressos
da Trigonometria esférica, até ao método actualmente
usado para determinar as latitudes por meio de
observações extra-meridianas do Sol.

D. João de Castro foi o maior dos discípulos de
Pedro Nunes e foi, como Duarte Pacheco, um cosmógrafo
insigne, um navegador notável e um grande capitão.
Camões glorificou-o no seu poema e Jacinto Freire de
Andrade descreveu a sua vida em linguagem clássica e
estilo conceituoso e brilhante.
Nas suas viagens fez o célebre Vice-Rei da Índia
numerosas observações de declinação magnética e
ainda de desvios da agulha devidos a curvas locais, por
meio do instrumento de sombra de Pedro Nunes, continuando
assim as observações da mesma natureza que tinham sido
feitas por João de Lisboa, como já dissemos, com um
aparelho rudimentar.
As observações de declinação magnética feitas por
estes dois navegadores formam a primeira contribuïção
notável ao problema da distribuïção geográfica das
linhas de igual declinação. Por meio das suas
observações mostrou ainda D. João de Castro que a
declinação magnética e a longitude dos lugares não
estão ligadas pela simples relação de
proporcionalidade que admitiam João de Lisboa e Rui
Faleiro, irmão de Francisco Faleiro.
Os resultados das suas observações foram
apresentadas por êle próprio, em três relatórios
publicados pela primeira vez no século XIX, sob os
títulos: Roteiro de Lisboa à Índia publicado em
1882; Primeiro Roteiro da Costa da Índia desde Goa a
Diu, publicado em 1843; Roteiro de Lisboa até
Suez publicado em 1833. São três obras importantes
para a história da Geografia.

É interessante o capítulo que no tratado De arte
atque ratione navigandi Pedro Nunes consagrou às
Tábuas de declinação do Sol.
Vimos anteriormente que estas Tábuas são
indispensáveis para o cálculo das latitudes por meio da
observação da altura do Sol e dissemos que nas
navegações portuguesas se construíam por meio do Almanach
de Zacuto. Neste Almanach encontram-se, como já
dissemos, Tábuas para determinar as longitudes do Sol
para todos os dias do ano 1473 e para os três anos
seguintes e regras para destas Tábuas tirar as que
convêm a outro ano qualquer, e encontra-se ainda outra
Tábua, semelhante a uma das Tábuas afonsinas, que dá o
valor das declinações dos astros correspondentes às
suas longitudes contadas de grau a grau, supondo a
obliqüidade da Eclíptica igual a 23° 33'.
Ora, Pedro Nunes substituíu a Tábua das
declinações de Zacuto, por outra correspondente à
obliquidade da Eclíptica de 23°30’. No Tratado
em defensam da carta de marear, tinha dado as Tábuas
de longitudes para os anos de 1537 à 1540.
Convém observar que Ptolomeu, seguindo Eratostenes e
Hiparco, adoptara para a obliqüidade da Eclíptica o
número 23°51’ e que, mais tarde, nos anos 829 e
830 depois de Cristo, os astrónomos de Bagdad, medindo-a
de novo cuidadosamente, obtiveram o número 23° 33', que
foi adoptado por Zacuto e pelos cosmógrafos portugueses
anteriores a Pedro Nunes. É estranhável que Zacuto não
tenha adoptado o número 23°32' 30", empregado nas
Tábuas afonsinas, que no seu tempo estava mais próximo
do verdadeiro do que o número que preferiu.
No século XVI já estes números não convinham e
Pedro Nunes adoptou o número 23° 30' empregado por
Regiomontano nas suas Efemérides.
Pelo que respeita à variação da linha dos
equinócios, aceitou Pedro Nunes a doutrina dos
astrónomos de Toledo, segundo a qual esta linha tem ao
mesmo tempo o movimento de precessão de Ptolomeu e o
movimento de trepidação de Azarquiel. É muito
interessante, sob o ponto de vista histórico-crítico, a
análise que o nosso douto matemático faz dos trabalhos
relativos a esta questão escritos desde o tempo de
Ptolomeu, demorando-se principalmente no comentário dos
que se devem aos astrónomos de Afonso X.
É estranhável que nesta matéria se não faça
menção do Almanach de Zacuto, que tão útil
fôra às navegações portuguesas. Eu penso, com o sr.
Joaquim Bensaúde, que talvez Pedro Nunes tenha tido
receio de afrontar o fanatismo dos cristãos do seu
tempo, mencionando um judeu que fôra recentemente
expulso de Portugal como rèprobo do verdadeiro Deus.
Talvez se refira ao célebre hebreu proscrito uma
passagem da obra a que nos estamos referindo, na qual se
fala de um varão deligentíssimo (vir deligentissimus)
na correcção dos tempos sem lhe mencionar o nome.
Também infelizmente o nosso matemático não fala nas
suas obras dos cosmógrafos portugueses do século XV,
a-pesar-de elogiar algumas vezes o que até ao seu tempo
se tinha feito em Portugal no que respeita à ciência e
arte de navegar, e por isso tem responsabilidade na
lenda, que correu durante séculos, da intervenção da
ciência germânica na náutica portuguesa.

Percorrendo as obras de Pedro Nunes, vê-se, e muitas
vezes, o seu engenho manifestar-se na invenção de
instrumentos astronómicos e de métodos gráficos ou
mecânicos para a resolução de diversos problemas
numéricos. Descreveremos nas Notas juntas a êste livro
o seu anel graduado, que goza da propriedade
notável de bastar dividir os seu quadrantes em quarenta
e cinco partes iguais, em vez de noventa, para obter o
valor dos ângulos que determina, expressos em graus, o
seu instrumento de sombras para a medida da altura
do Sol e o seu compasso, já mencionado, para o cálculo
dos senos com aproximação suficiente para os usos da
náutica. Aqui vamos sòmente considerar a peça que
juntou ao astrolábio náutico com o fim de medir
fracções do grau, conhecida entre nós pelo nome de
Nónio.
A invenção do Nónio foi sugerida a Pedro Nunes por
uma passagem do Almagesto pela qual se vê que os
antigos astrónomos, medindo o arco do meridiano
compreendido entre os trópicos, acharam que êste arco
está para a circunferência como 11 para 83, e portanto
que metade daquele arco, isto é, a obliqüidade da
Eclíptica, é igual a 23° 51’20’’ (2).
(2) Representando por
x a obliqüidade da Eclíptica, temos
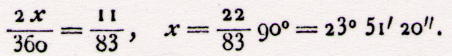
|
Para se explicar como se obteve para valor do
ângulo medido a fracção 11/83 da circunferência,
admitiu Nunes que no astrolábio empregado estava
traçada uma circunferência concêntrica com aquela em
que eram medidos os graus, que o seu quadrante estava
dividido em 83 partes iguais e que a linha de fé da
alidade do instrumento passava pela divisão 44.
Explicada assim a passagem considerada do Almagesto,
expôs o nosso geómetra, como conseqüência dela, o
seguinte modo de obter o valor dos ângulos por meio do
astrolábio.
Tracemos no instrumento 44 circunferências
concêntricas com a que mede os graus e dividamos o
quadrante de cada uma em, respectivamente, 89, 88, 87, .
. . partes iguais, sendo as divisões contadas a partir
do raio que passa pela origem da divisão da
circunferência que determina os graus. Mede-se depois o
ângulo dado pela circunferência que dá o seu valor com
maior aproximação.
Pedro Nunes não considera a sua doutrina sôbre a
medida dos ângulos como invenção própria, mas como
uma reconstituïção do método que julga ter sido
empregado por Ptolomeu para aquela medida.
O instrumento de Nunes foi notàvelmente simplificado
e tornado prático pelo Padre Cristóvão Clávio,
discípulo do matemático português, que no seu Astrolabium
livro publicado em 1593, substituíu as 44
circunferências de Nunes por um arco auxiliar de uma
única, dividido em 61 partes iguais e abrangendo um arco
de 60 graus do limbo do astrolábio(3),
e depois por
(3) Pode ver-se a
passagem do Astrolabium em que Clávio deu
a sua doutrina em um artigo de Breusing,
publicado no Jornal de Ciências Matemáticas (Coimbra,
1881, tômo III), e que Rodolfo Guimarães
transcreveu no Instituto de Coimbra (tômo XLIX,
1902), fazendo acompanhar a referida passagem da
tradução do latim para português.
|
Vernier, que em um livro publicado em 1631, sob
o título de Construction du quadrant noveau (4),
determinou o movimento do arco auxiliar, ligando-o à
alidade do astrolábio, com a qual se desloca. Destas
duas invenções resultou o instrumento actualmente
conhecido pelo nome de nónio ou vernier.
(4) Este opúsculo
é muito raro. Pode ver-se nos Anais da
Academia Politécnica do Pôrto (1916, tômo
XI) uma notícia bastante desenvolvida de um
exemplar que se encontra na Biblioteca Nacional
de Paris.
|
É instrutiva, a êste respeito, uma Nota do Ensaio
histórico de Garção Stockler, na qual êste
matemático indica um modo de passar do instrumento de
Nunes para o de Clávio e Vernier. Mas esta passagem não
se faz com tanta evidência que tire aos
aperfeiçoamentos dêstes últimos o seu mérito.
Explicar uma invenção feita é muito diferente de
inventar. E mesmo não é crível que Clávio e Vernier
seguissem caminho tão longo para chegar a uma invenção
que se lhes apresentou de uma maneira bem simples.
O que podemos dar como certo é que Pedro Nunes,
inspirado por Ptolomeu, pôs o problema da avaliação
das fracções do grau nas medições feitas com o
astrolábio e deu a primeira solução dêle, e que outra
solução, simples e prática, foi depois dada por
Clávio e Vernier e que ao primeiro dêstes matemáticos
pertence a idea essencial desta solução.
A respeito da passagem do tratado De arte atque
ratione navigandi em que Pedro Nunes se referiu à
invenção do seu instrumento, faremos aqui algumas
observações.
Ptolomeu fala da obliqüidade da Eclíptica no
Almagesto (pág. 9 da edição de 1515), mas não diz que
foi êle quem encontrou a fracção  da circunferência, para valor do
arco do meridiano compreendido entre os trópicos. Dá o
modo de obter êste ângulo e diz que o seu valor está
compreendido entre da circunferência, para valor do
arco do meridiano compreendido entre os trópicos. Dá o
modo de obter êste ângulo e diz que o seu valor está
compreendido entre 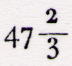 e e 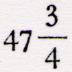 do grau, isto é, entre 47°40' e 47°45'.
Depois acrescenta que a esta condição satisfaz o valor do grau, isto é, entre 47°40' e 47°45'.
Depois acrescenta que a esta condição satisfaz o valor  da circunferência obtida
por Eratóstenes (que chama Archusiano) e Híparco (que
chama Abrachis). Diz ainda que o limbo do instrumento
deve ser dividido em graus e cada grau em partes do grau,
sem fixar o número delas. A nos parece-nos que uma
hipótese possível para explicar os números obtidos
para o valor do arco compreendido entre os trópicos é
que cada grau do instrumento estava dividido em doze
divisões de 5' cada uma e assim obteria que o valor do
ângulo considerado está entre 47° mais oito divisões
do grau e 47º mais nove divisões do grau. Poderia
também cada grau estar dividido em seis partes de 10º
cada uma e calcular as meias divisões por aritmética. da circunferência obtida
por Eratóstenes (que chama Archusiano) e Híparco (que
chama Abrachis). Diz ainda que o limbo do instrumento
deve ser dividido em graus e cada grau em partes do grau,
sem fixar o número delas. A nos parece-nos que uma
hipótese possível para explicar os números obtidos
para o valor do arco compreendido entre os trópicos é
que cada grau do instrumento estava dividido em doze
divisões de 5' cada uma e assim obteria que o valor do
ângulo considerado está entre 47° mais oito divisões
do grau e 47º mais nove divisões do grau. Poderia
também cada grau estar dividido em seis partes de 10º
cada uma e calcular as meias divisões por aritmética.
Agora vem outra questão: como encontraram
Eratóstenes e Híparco o número  ? ?
Segundo Pedro Nunes, que não cita estes autores e o
atribui a Ptolomeu, teria sido obtido, como dissemos, por
meio de um círculo cujo quadrante estava dividido em 83
partes iguais.
Delambre, na sua Histoire de l'Astronomie,
considera a questão e sem mencionar o nosso matemático,
apresenta outra explicação. Diz que por meio do
instrumento se achou que o ângulo considerado está
compreendido entre 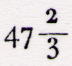 e e
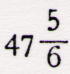 do grau, e portanto entre os números do grau, e portanto entre os números
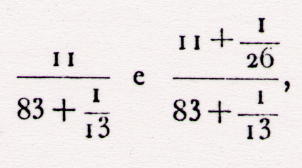
que são aproximadamente iguais a  . .
Nós, atendendo ao facto de Ptolomeu falar da divisão
do limbo do astrolábio em partes de grau, aceitamos a
opinião de Delambre, modificando-a de modo a
harmonizá-la com os números dados por Ptolomeu para
limites entre os quais está o valor do arco de círculo
máximo compreendido entre os trópicos. Com efeito, em
vez de dizer, com Delambre, que êste valor está
compreendido entre 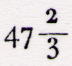 e e 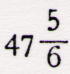 da
circunferência, diremos que está compreendido entre da
circunferência, diremos que está compreendido entre 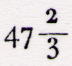 e e 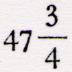 da circunferência e que da circunferência e que 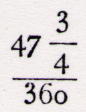 se pode considerar como
igual a se pode considerar como
igual a  com um
êrro inferior a com um
êrro inferior a 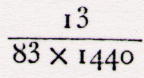
Não sabemos se Pedro Nunes fêz construir o seu
instrumento. Segundo uma tradição colhida por Stockler,
os instrumentos astronómicos que existiam na
Universidade de Coimbra foram fundidos no período de
decadência científica que se seguiu à morte de Nunes
para se aplicar o seu metal na construção de uma grade.
O único exemplar dêste instrumento de que há notícia
foi mandado construir por Tycho-Brahe, mas êste
astrónomo renunciou em breve ao seu emprêgo por não
lhe reconhecer utilidade prática. Mais tarde, Delambre
notou na Histoire de l'Astronomie, com o exame de
uma série de casos, a dificuldade na escolha do círculo
que se deve empregar para medir cada ângulo. Felizmente
a invenção do matemático português levou à de
Clávio e depois ao precioso instrumento de Vernier.
Tem-se discutido muito se ao instrumento actualmente
empregado para medir as sub-divisões do grau se deve dar
o nome de nónio ou o de vernier.
A mim não me agrada nem a primeira nem a segunda
designação. Quem lhe chama nónio não diz a
verdade; quem lhe chama vernier não é justo.
Além disso, considero o uso de designar nas ciências um
objecto com o nome de um homem como inconveniente para a
sua história, por levar muitas vezes a ideas falsas a
respeito das invenções. O caso actual é um dêles. Nem
é històricamente justa a designação de nónio,
nem a de vernier. Eu preferiria chamar aos
instrumentos considerados sub-divisores dos ângulos,
e então figurariam na história o do nosso matemático
com o nome de sub-divisor de Nunes e o actual com
o nome de sub-divisor de Clávio e Vernier, porque
estes nomes não podem separar-se na invenção dêste
sub-divisor.
|
![]()
![]()
![]()
![]()
![]() da circunferência, para valor do
arco do meridiano compreendido entre os trópicos. Dá o
modo de obter êste ângulo e diz que o seu valor está
compreendido entre
da circunferência, para valor do
arco do meridiano compreendido entre os trópicos. Dá o
modo de obter êste ângulo e diz que o seu valor está
compreendido entre ![]() e
e ![]() do grau, isto é, entre 47°40' e 47°45'.
Depois acrescenta que a esta condição satisfaz o valor
do grau, isto é, entre 47°40' e 47°45'.
Depois acrescenta que a esta condição satisfaz o valor ![]() da circunferência obtida
por Eratóstenes (que chama Archusiano) e Híparco (que
chama Abrachis). Diz ainda que o limbo do instrumento
deve ser dividido em graus e cada grau em partes do grau,
sem fixar o número delas. A nos parece-nos que uma
hipótese possível para explicar os números obtidos
para o valor do arco compreendido entre os trópicos é
que cada grau do instrumento estava dividido em doze
divisões de 5' cada uma e assim obteria que o valor do
ângulo considerado está entre 47° mais oito divisões
do grau e 47º mais nove divisões do grau. Poderia
também cada grau estar dividido em seis partes de 10º
cada uma e calcular as meias divisões por aritmética.
da circunferência obtida
por Eratóstenes (que chama Archusiano) e Híparco (que
chama Abrachis). Diz ainda que o limbo do instrumento
deve ser dividido em graus e cada grau em partes do grau,
sem fixar o número delas. A nos parece-nos que uma
hipótese possível para explicar os números obtidos
para o valor do arco compreendido entre os trópicos é
que cada grau do instrumento estava dividido em doze
divisões de 5' cada uma e assim obteria que o valor do
ângulo considerado está entre 47° mais oito divisões
do grau e 47º mais nove divisões do grau. Poderia
também cada grau estar dividido em seis partes de 10º
cada uma e calcular as meias divisões por aritmética. ![]() ?
? ![]() e
e
![]() do grau, e portanto entre os números
do grau, e portanto entre os números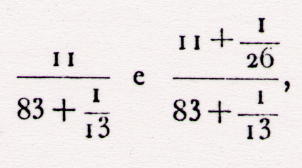
![]() .
.![]() e
e ![]() da
circunferência, diremos que está compreendido entre
da
circunferência, diremos que está compreendido entre ![]() e
e ![]() da circunferência e que
da circunferência e que ![]() se pode considerar como
igual a
se pode considerar como
igual a ![]() com um
êrro inferior a
com um
êrro inferior a ![]()